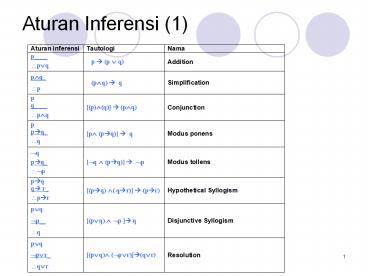
Aturan Inferensi (1)

1
Aturan Inferensi (1)
2
Aturan Inferensi (2)

• ?x P(x) Universal instantiation
• ?P(c)
• P(c) utk setiap c Universal generalization
• ? ?x P(x)
• ?x P(x) Existential
  instantiation
• ?P(c) utk suatu c
• P(c) utk suatu c Existential
  generalization
• ? ?x P(x)

3
Metode Pembuktian (1) Bukti langsung dan Tak
langsung

• Bukti Langsung
• Implikasi p ? q dapat dibuktikan dengan
  menunjukkan jika p benar maka q juga harus benar.
• Soal 9. Berikan bukti langsung dari
• Jika n bilangan bulat ganjil maka n2 ganjil.

• Bukti Tak langsung
• Karena p ? q ekivalen dengan ?q ? ?p maka
• p ?q dapat dibuktikan dengan menunjukkan bhw
• ?q ? ?p benar.
• Soal 10. Berikan bukti dari
• Jika n2 ganjil maka n ganjil.

4
Bukti kosong dan bukti trivial

• Bukti kosong
• Jika hipotesis p dari implikasi p ? q salah, maka
  p ? q selalu benar, apapun nilai kebenaran dari
  q.
• Contoh. P(n) Jika n gt 1, maka n2 gt 1.
• Tunjukkan P(0) benar.

Bukti trivial Jika konklusi q dari implikasi p ?
q benar, maka p ? q selalu benar, apapun nilai
kebenaran dari p. Contoh. P(n) Jika a, b
integer positif dengan a ? b, maka an ?
bn. Tunjukkan P(0) benar.
5
Metode Pembuktian (2)Bukti dengan kontradiksi

• Tunjukkan bahwa sedikitnya ada 4 hari yang sama
  dari pilihan 22 hari sebarang.
• Buktikan bahwa ?2 irasional.
• bukti tak langsung bukti dg kontradiksi
• Tunjukkan bahwa jika n2 ganjil maka n ganjil.

6
Metode Pembuktian (3)Bukti eksistensi

• Bukti Eksistensi Konstruktif
• Tunjukkan bahwa ada bilangan bulat positif yang
  dapat dituliskan sebagai jumlah dua bilangan
  pangkat 3.
• Solusi. 1729 103 93 123 13.
• Tunjukkan bahwa ada bilangan bulat positif yg
  sama dengan jumlah bilangan-bilangan bulat
  positif yg tidak melebihinya.

• 2. Bukti Eksistensi Nonkonstruktif
• Tunjukkan bhw ada bilangan irrasional x dan y
  sehingga xy rasional.
• Solusi. Kita tahu bahwa ?2 irrasional. Pandang
  ?2?2. Jika ia rasional maka terbukti.
• Jika tidak, perhatikan (?2?2)?2 ?222.
• Jadi terbukti ada pasangan (x?2, y ?2) atau (x
  ?2?2 dan y ?2) yg salah satunya memenuhi xy
  rasional.

7
Metode Pembuktian (4)Bukti ketunggalan

• Ada 2 bagian dalam bukti ketunggalan
• Menunjukkan bahwa ada elemen x yg memenuhi sifat
  yg diinginkan. (existence)
• Menunjukkan bahwa jika y ? x maka y tidak
  memenuhi sifat yg diinginkan. (uniqueness)

• Contoh. Tunjukkan bahwa setiap bilangan bulat
  mempunyai invers penjumlahan yang tunggal.
• Solusi. Jika p bulat maka pq 0 ketika q -p,
  dan q juga bulat.
• Untuk menunjukkan ketunggalan, misalkan ada r
  bulat dengan r ? q dan pr0. Maka pq pr.
• Dengan mengurangi kedua ruas dgn p didapat qr,
  kontradiksi dgn r ? q. Jadi ada bilangan bulat q
  yang tunggal sehingga pq0.

8
Metode Pembuktian (5)Contoh Penyangkal (Counter
Example).

• Tunjukkan bahwa pernyataan
• setiap bilangan bulat positif adalah hasil
  tambah dari tiga bilangan kuadrat
• adalah salah.
• Solusi. Pernyataan ini benar untuk beberapa
  nilai, mis.
• 1020212 2021212 3121212 4020222
  5021222 6121222 .
• Tapi kita tidak dapat mengekspresikan seperti di
  atas untuk bilangan 7.
• Jadi bilangan 7 merupakan contoh penyangkal dari
  pernyataan di atas.