Exercice n1 pb3

1
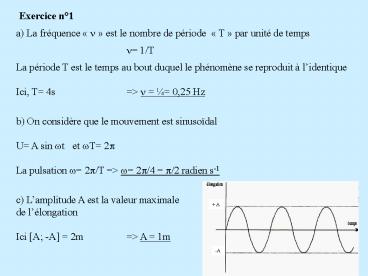
Exercice n1
a) La fréquence  n  est le nombre de période
 T  par unité de temps n 1/T La période T
est le temps au bout duquel le phénomène se
reproduit à lidentique Ici, T 4s gt n ¼
0,25 Hz b) On considère que le mouvement est
sinusoïdal U A sin wt et wT 2p La pulsation
w 2p/T gt w 2p/4 p/2 radien s-1 c)
Lamplitude A est la valeur maximale de
lélongation Ici A -A 2m gt A 1m
A
-A
2
d) La vitesse de propagation célérité  c  de
londe c ln Où l longueur donde
distance parcourue par londe pendant une
période Ici l distance entre 2 crêtes de
vagues 30m c ln 30 . 0,25 7,5 m s-1
3
Exercice n2

• a) Quelles est lintensité dun son de 40dB?
• Lintensité dun son ou puissance surfacique
  w  dun son est défini par
• w v p elle est exprimée en Wm-2
• avec v vitesse de vibration en un point, p
  pression accoustique
• et p v r c où p en P, v vitesse, r
  masse volumique, c célérité
• On peut aussi exprimer lintensité dun son en dB
  pour facilité les calculs, en prenant comme
  référence la puissance surfacique w0
  correspondant au seuil de laudition à 1000Hz,
  avec
• W0 10-12 Wm-2 10-16 Wcm-2
• On a alors I dB 10 log10 w/w0
• Application numérique
• 40DB 10 log10 w/w0 gt log10 w/w0 4
• w/w0 104
• W 104 w0 , doù w 10-12 Wcm-2

4
b) Combien de violonistes pour obtenir un son de
60 dB? Lintensité du son produit par n
violoniste n.w gt 60dB 10 log10 nw/w0 gt
log10 nw/w06 gt (log10 n) (log10 w/w0) 6
et log10 w/w0 4 gt log10 n 6- 4 gt n 102
100 violonistes c) La sonie est la sensation de
force dun son perçu par loreille Par
convention Un son de X dB à 1000Hz a un niveau
de X phones Un son de X phone provoque, quelque
soit sa fréquence, une sensation de force (ou
sonie) correspondant à celle dun son de X dB à
1000Hz
5
Utilisation des courbes isosoniques de Fechner et
Munson
Chaque son est défini par sa fréquence en Hz et
son intensité en dB, la courbe donne la sonie
correspondante Pour 1 violoniste , on a 200 Hz
et 40dB gt 20 phones Pour 100 violonistes
, on a 200 Hz et 60dB gt 50 phones
6
Chaque son est défini par sa fréquence en Hz et
son intensité en dB, la courbe donne la sonie
correspondante Pour 3200 Hz avec 1 violoniste
, on a 3200 Hz et 40dB gt 40 à 50 phones
Avec 100 avec violonistes , on a 3200 Hz et
60dB gt 60 à 70 phones
7
Exercice n3 40dB à 1m , Quelle distance pour
que I 20dB Utilisation de la loi de linverse
du carré de la distance W2/W1
d12/d22 Calcul des intensité en w m-2
I1 10 log10 w1/w0 40dB gt w1/w0 104 et
w1 104w0 I2 10 log10 w2/w0 20dB gt w2/w0
102 et w2 102w0 gt w2/w1 102w0 / 104w0
d12/d22 gt w2/w1 102/ 104 12/d22 gt d2
10m
2
1
S
d1
d2
8
Exercice n4 Lintensité sonore dune machine est
de 21 dB, combien de machines pour ne
pas Dépasser 30 dB? Pour une machine 21dB 10
log10 w1/w0 gt log10 w1/w0 2,1 Pour n machines
30 dB 10 log10 nw1/w0 (log10 n) (log10
w1/w0 ) 3 gt log10 n 3- 2,1 gt n 100,9
8 machines
9

• Exercice n5
• R 0,007 et T 0,993
• 99,3 du faisceau va être transmis en profondeur
  ce qui permettra une bonne
• détection en profondeur
• La graisse nest pas un obstacle à la réalisation
  dune échographie
• b) R (Z2-Z1) / (Z1Z2)2
• Milieu1 graisse
• Milieu2 muscle
• R (Z2-Z1) / (Z1Z2) gt Z2-Z1 R (Z1Z2)
• Z1 Z2 ((1- R)/ (1 R)) et R 0,007
• Z2 1,6 105 g cm-2 s-1
• gt Z1 1,354 105 g cm-2 s-1

10
Exercice n6 On définie la loi datténuation
I (x) I0 e-ax Avec I (x) intensité à
la profondeur x en w.m-2 I0 intensité initiale
du faisceau a coefficient datténuation par
absorption ou pouvoir de pénétration, m-1 a)
Quelle est lépaisseur  x  pour avoir une
atténuation de 50 Atténuation de 50 gt I (x)
/ I0 0,5 gt e-ax 0,5 gt x -(ln 0,5)/a
(ln2)/0,15 x 4,62 cm b) La source est
ponctuelle gt le faisceau est divergent gt il
existe également une atténuation en rapport avec
cette divergence gt la loi de linverse du carré
de la distance I2/I1 d12/d22
11
Ici d1 1cm d2 5cm I1 I0 0,02 w
cm-2 Et donc I I0/ d2 2 Si on considère
latténuation due à la fois à la divergence et
aux tissus, On a I I0/ d2 2 . e-ax avec
x 5- 1 4cm gt I 4,39 10-4 w cm-2
2
1
S
d11
d2 5
12
Exercice n7 Dn 2 v . cos q .n0 /c où v
vitesse de déplacement du sang
q angle formé entre le faisceau et la
direction découlement du sang v c Dn / 2
cos q .n0 avec n0 5MHz q 60 Dn 974
Hz et c 1540ms-1 gt v 0,299 ms 1
n1
n0
13

• Exercice n8
• Effets doppler Fizeau
• Définition il sagit dune modification de
  fréquence lorsque la source et/ou le récepteur
  sont
• en mouvement
• Ici nous sommes dans le 1ier cas
• source mobile/observateur immobile, v est
  positive de S vers O
• La fréquence observée n est reliée à la
  fréquence démission n par la formule
• n n ( c / (c-v))
• Si v est lt0 (source qui séloigne) n lt n
• Si v est gt0 (source qui se rapproche) n gt n
• a) La source se rapproche de lobservateur
• gt Par convention v est positive
• n n ( c / (c-v)) gt 1000. 344 / (344 15)
  1046 Hz
• b) La source séloigne de lobservateur
• gt Par convention v est négative