CONTOUR MAPS INTRODUCTION

1
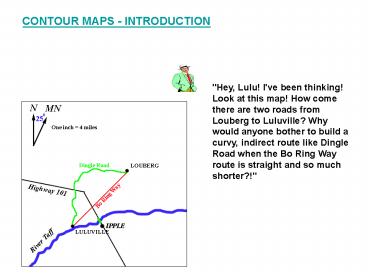
CONTOUR MAPS - INTRODUCTION
"Hey, Lulu! I've been thinking! Look at this map!
How come there are two roads from Louberg to
Luluville? Why would anyone bother to build a
curvy, indirect route like Dingle Road when the
Bo Ring Way route is straight and so much
shorter?!"
2
"Look at my map and you'll see!"
"Wow! Cool map! Dingle Road must have been easier
to build! It must be old! Old but scenic! It goes
around all the hills! Bo Ring Way goes up, over
and through the mountains! A miracle of modern,
fast highway building! But a little dull! I
really like those 3-D effects on your map, Lulu!"
3
"The map has its good points! But it doesn't tell
you how high or steep the mountains are! And you
can't see what's going on on the sides of the
mountains facing away from us!"
"True, true! But whad'ya gonna do?!"
"Get a map with topographic contours! A contour
map!"
4
"Take it step by step, Lou, step by step! Take a
look at this picture!"
"The heights above sea level (that is, the
elevations) of the three peaks are 3047 feet for
Mt. Riddle, 3998 feet for Mt. Ginger, and 2186
feet for Mt. Tipster!"
"An island paradise! Three peaks, rivers flowing
down to the sea! Very exotic!"
ROLLOVER
5
"That guy with the paintbrush sure had a lot of
energy! What do you call those lines?"
"Those lines are called contour lines! They're
lines of equal elevation above sea level! All the
points on the lowest line are zero feet above sea
level! All the points on the next higher contour
line are 500 feet above sea level! And so on!"
"That sounds cool!"
6
"Hold on, Lou! That's not all! Then the guy flew
over the island and looked straight down from way
up high, and this is what he saw!"
"All the painted shorelines - and the rivers!
Like a map!"
"Right on, Louis! A CONTOUR MAP! Now we're in a
position to 'see' the shape of the island and the
elevation of any place on its surface!
7
LABELING CONTOURS
"So here we are, Lou! Here's our island with all
the lines of equal elevation painted on it! The
contour lines!"
"And here's what the island looks like looking
down at it from way up in the air!"
8
"Now pay attention to this, Lou! If we want to
know the elevation of any of the lines, all we
have to remember is that the first one (the one
on the outside) was at sea level - elevation 0'!
And because we pretended that sea level rose by
500 feet each time, as we go inland, away from
the sea, each line that we hit is 500 feet higher
than the one before!"
"What we have is a contour map! The painted lines
are topographic contours lines of equal
elevation (height above sea level). So, we have
contours at 0', 500', 1000' and so on. We have no
contours above 3500' because the highest point on
the island, the peak of Mt Ginger, is only
3998'above sea level! It never reaches 4000',
which would be the next contour!"
9
"If we had made sea level 'rise' by 250 feet each
time (instead of 500 feet), we would have had
twice as many contours! They would have been at
0', 250', 500' and so on! "
 "But you can see it gets to be a bit messy, what
with all those numbers! Instead of labeling every
line, we can let everyone know the vertical
distance between the contour lines! We call that
the contour interval, abbreviated C.I.!"       
"Then all we do is label every fifth contour,
starting with the zero contour. We also make the
labeled lines heavier! People can do the counting
on their own and the map is easier to see!"     
  "Notice, by the way, that the elevations of
contour lines are always whole number multiples
of the contour interval! If the C.I. is 250',
then there are contours at 0 x 250' (0') 1 x
250' (250') 2 x 250' (500') 3 x 250'
(750')....! If the C.I. was 20', then there
would be contours at 0 x 20' (0') 1 x 20'
(20') 2 x 20' (40').... Get it?!"
10
"I get it! Putting it another way, if you take
the elevation of a contour line and divide it by
the C.I., the answer must be a whole number! For
example, if the C.I. is 40', then you can have a
contour at 1800' (1800'/40' 45), but not at
1900' (1900'/40' 47.5')!"
"But I have this question! How do you know what
contour interval to use when you're making a
map??!"
"Good question!! You choose a contour interval
small enough to show things that are important to
you, but not so small as to make the map
illegible! In an area with little relief, you use
a small contour interval, otherwise nothing shows
up on the map! For an area with great relief, you
use a large contour interval so that you don't
obscure all the features in a sea of contour
lines! For maps where part of the region is flat
and part is rugged, then you can use different
contour intervals for different parts of the map!
But that's not done too often!"
11
"But I have another question! I can see that we
know the elevation of any place that falls right
on a contour line, but how do we know the
elevations of places that are not right on a
contour line?!"
"You can't know their elevations exactly, but
I'll show you what you can do! First you have to
figure out the elevations of the contour lines
between which the place lies. Look at point A! It
lies between the zero contour and the 250 foot
contour lines! If you think about our story of
sea level rising, you can see that A would get
drowned before the 250 foot level was reached! So
A is greater than zero but less than 250 feet! In
the same way, B is between 1750 and 2000 feet! As
for C, it lies above 3000 feet - and since there
is no 3250 foot contour there, it means C must be
less than 3250 feet!"
"And this is what it looks like on the contour
map!"
12
"And of course, all the points (brown dots) that
lie right on the contour lines have the elevation
of the contour line! I can see that! But how much
higher than 800' can the red dots be?!! And how
much lower than 700' can the green dots be?"
"Notice, by the way, that any place inside a
contour line is HIGHER than the contour line! And
any place outside a contour line is LOWER than
the contour line! So, since the green dots are
outside the 700' contour, their elevations are
less than 700'. The blue dots are inside the 700'
contour and so are higher than 700'. But the blue
dots are also outside the 800' and so are lower
than 800. That is, the blue dots are between 700'
and 800'. And the red dots are inside the 800'
and so are higher than 800."
13
"Well, since the contour interval (C.I.) is 100
feet, the next higher contour would be the 900
foot! But because there is no 900' contour, the
land must never get that high! If the contours
could be there, they would be there! Contours are
never left out! So the red dots can be any value
that is greater than 800 feet and less than 900
feet."
"Similarly, because there is no 600 foot contour,
the land must never get that low! If the contours
could be there, they would be there! Contours are
never left out! So the green dots can be any
value that is less than 700 feet and more than
600 feet!"
14
(No Transcript)
15
"Let's look at a bigger area now! You can see
that there are two separate 700' contours, one
around Mt. Tom and one around Mt. Tim! You can
see that Mt. Tim never reaches 800 feet as
there's no 800' contour there! And Woodland
Valley never gets as low as 600 feet otherwise
there would be a 600' contour! "
"This is driving me dotty! But where are all the
lower contours? The zero, the 100', the 200' and
so on?!"
16
THE RULE OF V'S
17
(No Transcript)
18
RELIEF
19
(No Transcript)
20
DEPRESSION CONTOURS
"Now take a look at this contour map of the
volcano! What's wrong with it, Lou?"
"The contours on the outside of the volcano
between the 517' point on the plain and the 1397'
on the rim are OK! But at the top of the volcano
they go crazy! You've got a 1200' inside a 1200'
and a 1000' contour inside a 1200'! And we know
that everything inside a contour is supposed to
be higher than the contour!"
21
"Keerect, Lou! So look what we've done - we've
made up a new type of contour, called a
DEPRESSION CONTOUR! It's marked with little
'teeth' called HACHURES! For hachured contours, a
point inside a contour is lower than the contour!
And a point outside a contour is higher than the
contour! Just the opposite of ordinary,
unhachured contours!"
"Clever! So if we look at the top of the volcano,
the 1397' on the rim is inside the ordinary 1200'
contour and is higher than the contour - which is
as it should be - and at the same time is outside
the hachured 1200' contour and is higher than it
- which is as it should be! And the hachured
1000' contour is inside and lower than the
hachured 1200' contour, and the 872' bottom of
the crater is inside and lower than the hachured
1000' contour! Again, as it should be! Neat-o!!
From the rim, the land goes down on both sides -
towards the outside of the volcano and towards
the crater!"
22
(No Transcript)
23
(No Transcript)
24
CONTOUR SPACING AND STEEPNESS
"So you want to know how steep the journey's
going to be, eh, Lou?! Let's go back and look at
our island! You notice how the slope from the top
of Mt. Tipster down to the sea is much steeper
than the slope from the top of Mt. Riddle down to
the sea?!"
"Now look at the contour map! Where the slopes
are steeper, the contour lines are closer
together! Where the slopes are gentler, the
contours lines are further apart!"
25
"Gotcha!! But what happens if you have a cliff -
a vertical cliff?! Like on this island I've drawn
showing some contours!"
"Glad you're learning to draw, Lou! Well, in that
case, on the map, the contours come together and
merge! But otherwise, unless there's a cliff,
contours never touch or cross each other!"
26
"But don't go too far with it, Lou! On the maps
we've been looking at, you can see where it's
steeper and gentler, but not how steep or gentle
(except where it's vertical)! To really know how
steep or gentle the slopes are, you need to know
the distance (scale) and the contour interval! I
mean, if the island is ten miles across and the
highest point is only five feet above sea level,
then even the steepest part is going to be pretty
flat! You need a map more like this one! Now you
can see how much you go up in a given horizontal
distance!!"
27
GRADIENT
"What you need to know, Lou, is the gradient!
Gradient tells you how steep your route is!
Gradient can be expressed numerically in many
ways. One common way to describe the average
steepness or gradient between two points is to
state the difference in elevation (ED) divided by
the horizontal distance (HD) GRADIENT ED/HD
Take a look at this example The vertical
distance (here, the difference in elevation
between points 'A' and 'B') 10,000 feet The
horizontal distance from 'A' to 'B' 5 miles
Gradient vertical distance (elevation
difference (ED)) divided by horizontal distance
(HD) The GRADIENT is 2000 feet per mile (10,000
feet divided by 5 miles) Elevation difference may
also be expressed in inches, meters or some other
convenient unit similarly, horizontal distance
may be expressed in feet, kilometers, etc. Thus,
the gradient may be stated as inches/foot,
feet/mile, meters/kilometer, etc.
28
The diagram below shows some slopes and their
approximate gradients in feet/mile.
29
"Gradient can be calculated from contour maps!
Suppose you plan to 'bushwack' in a straight line
from 'A' to 'B' and want to know how steep it
will be. 'A' falls on the 2500' contour 'B'
falls on the 1250' contour. So the elevation
difference (vertical distance) is 1250'. The
horizontal distance from 'A' to 'B' can be gotten
from the scale! The distance on the map from 'A'
to 'B' is 1 inch! On the ground, that five
miles! So, the gradient is 1250'/5 miles! Divide
through, and you get 250 feet per mile!"
30
"And let's suppose you wanted to work your way up
the river, from 'D' to 'C'! You can get the
gradient of the river in the same way! Point 'C'
lies half way between the 1750' and 2000'
contours, so we can estimate its elevation as
midway between the two contours 1875'. The
elevation of 'D' is 0', because it lies at sea
level. So, the elevation difference between C and
D is 1875' minus 0' 1875'! The horizontal
distance along the river is about twice the
length of the scale bar. Since the scale bar is 5
miles, twice its length is ten miles. So, the
gradient along the river is 1875'/10 miles
about 188' per mile!"
31
"But the spacing of the contours and the gradient
vary as you go along the river!"
"You're right, Lou! The gradient you get this way
is only the AVERAGE GRADIENT! Also, there's no
way of knowing what the gradient is between
contours! The contour interval is 250', so there
could be a hundred foot waterfall and then a
fairly level stretch between two of the contours
and they wouldn't show on the map! But it gives
you a general idea of what you'll encounter!"
                                                
                                                  
          ltgt