Variance functions or modelling heteroscedasticity

1
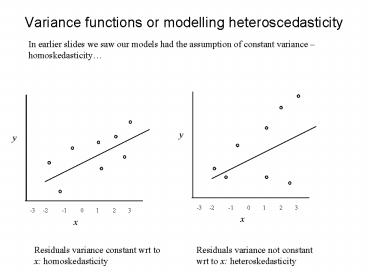
Variance functions or modelling heteroscedasticity
In earlier slides we saw our models had the
assumption of constant variance
homoskedasticity
-3 -2 -1 0 1 2
3
Residuals variance constant wrt to x
homoskedasticity
Residuals variance not constant wrt to x
heteroskedasticity
2
A simple case of heteroskedasticity
In the educational data set we have been working
with. Tabulating normexam by gender we see that
the means and variances for boys and girls are
(0.140 and 1.051) and (0.093 and 0.940). We may
want to fit a model that estimates separate
variances for boys and girls. The notation we
have been using so far assumes a common
intercept(?0) and a single set of student
residuals, ei, with a common variance ?e2. We
need to use a more flexible notation to build
this model.
3
Working with general notation in MLwiN
A model with no variables specified in general
notation looks like this.
A new first line is added stating that the
response variable follows a Normal distribution.
We now have the flexibility to specify
alternative distributions for our response. We
will explore these models later. The ?0
coefficient now has an explanatory x0 associated
with it. The values x0 takes determines the
meaning of the ?0 coefficient. If x0 is a vector
of 1s then ?0 will estimate an intercept common
to all individuals, in the absence of other
predictors this would be the overall mean. If x0
variable, say 1 for boys and 0 for girls, then ?0
will estimate the mean for boys.
4
A simple variance function
The new notation allows us to set up this simple
model where x0i is a dummy variable for boy and
x1i is a dummy variable for girl. This model
estimates separate means and variances for the
two groups. This is an example of a variance
function because the variance changes as a
function of explanatory variables. The function
is
5
Deriving the variance function
We arrive at the expression
(1)
6
Variance functions at level 2
The notion of variance functions is powerful and
not restricted to level 1 variances we have met
level 2 variance function already.
The random slopes model fitted earlier produces
the following school level predictions which show
school level variability increasing with intake
score.
The model
7
Two views of the level 2 variance
Given x0 1, we have
Which shows that the level 2 variance is
polynomial function of x1ij

• View 1 In terms of school lines predicted
  intercepts and slopes varying across schools.

  View 2  In terms of a variance function which
shows how the level 2 variance changes as a
function of 1 or more explanatory variables.
8
Elaborating the level 1 variance
Maybe the student level departures around their
schools summary lines are not constant.
Note at level 2 we have 2 interpretations of
level 2 random variation, random coefficients
(varying slopes and intercepts across level 2
units) and variance functions. In each level 1
unit, by definition, we only have one point,
therefore the first interpretation does not exist
because you cannot have a slope given a single
data point.
9
Variance functions at level 1
If we allow standlrt(x1ij) to have a random term
at level 1, we get
10
Modelling the mean and variance simultaneously
In our model
11
MM Opening up new types of research question
Multilevel approach allows modelling of mean and
variance simultaneously.
Illustrate by an analysis exploring the sources
of differential parenting. Why do parents treat
siblings differently?
Understanding the sources of differential
parenting the role of child and family level
effects. Jenny Jenkins, Jon Rasbash and Tom
OConnor Developmental Psychology 2003(1) 99-113
12
Is there a family effect?
Recent studies in developmental psychology and
behavioural genetics emphasise non-shared
environment and genetic influences are much more
important in explaining childrens adjustment
than shared environment has led to a focus on
non-shared environment.(Plomin et al, 1994
TurkheimerWaldron, 2000)
13
Differential parental treatment

• One key aspect of the non-shared environment that
  has been investigated is differential parental
  treatment of siblings.
• Differential treatment predicts differences in
  sibling adjustment
• What are the sources of differential treatment?
• Child specific/non-shared age, temperament,
  biological relatedness
• Can family level shared environmental factors
  influence differential treatment?

14
Parents have a finite amount of resources in
terms of time, attention, patience and support to
give their children. In families in which most of
these resources are devoted to coping with
economic stress, depression and/or marital
conflict, parents may become less consciously or
intentionally equitable and more driven by
preferences or child characteristics in their
childrearing efforts. Henderson et al
1996.This is the hypothesis we wish to test. We
operationalised the stress/resources hypothesis
using four contextual variables socioeconomic
status, single parenthood, large family size, and
marital conflict
The Stress/Resources Hypothesis
Do family contexts(shared environment) increase
or decrease the extent to which children within
the same family are treated differently?
15
A multilevel analysis
A model for the mean and a model for the
variability around the mean.
positive parenting
Overall mean
Family means
(between family variance)
Child specific parenting scores vary around
family mean(between child within family variance)
the within family variance is a measure of
differential parental treatment.
16
Modelling the mean and variance simultaneously
We show a possible pattern of how the mean,
within family variance and between family
variance might behave as functions of HSES in the
schematic diagram below.
Here are 5 families of increasing HSES(in the
actual data set there are 3900 families.
We can fit a linear function of SES to the mean.
positive parenting
The family means now vary around the dashed trend
line. This is now the between family variation
which is pretty constant wrt HSES
HSES
However, the within family variation(measure of
differential parenting) decreases with HSES
this supports the SR hypothesis.
17
Full Combined model for mean and variance

• We then allow the level 1 variance to be a
  function of the family level variables household
  socioeconomic status, large family size, and
  marital conflict. That is

Reduction in the deviance with 7df is 78.
18
Graphically
19
Conclusion for differential parenting

• We have found strong support for the
  stress/resources hypothesis. That is although
  differential parenting is a child specific factor
  that drives differential adjustment, differential
  parenting itself is influenced by family as well
  as child specific factors.
• This challenges the current tendency in
  developmental psychology and behavioural genetics
  to focus on child specific factors.
• Multilevel models fitting complex level 1
  variation needs to be employed to uncover these
  relationships.