PowerPoint-Pr

1
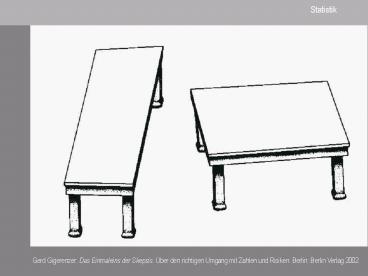
Statistik
Gerd Gigerenzer Das Einmaleins der Skepsis. Über
den richtigen Umgang mit Zahlen und Risiken.
Berlin Berlin Verlag 2002.
2
Statistik
Drei Weiterentwicklungen eines Rechners, zunächst
Benchmark-Ergebnis 9.3, dann 9.9, 10.3, 10.4
keine überzeugende Bilanz!
Norbert Schmitz Statistik Fehler, Fallen,
Schwindel. A. Lehmann, F. Lehmann (Hrsg.)
Messung, Modellierung und Bewertung von
Rechensystemen. 6. GI/ITG-Fachtagung, Neubiberg
1991, Proceedings, Berlin u.a. Springer 1991,
S. 1-14.
3
Statistik
... um Platz zu sparen Abschneiden des
unteren Teils der Ordinate.
4
Statistik
.... Strecken der Ordinate.
5
Statistik
.... es ist ja nicht viel Zeit vergangen
zwischen 3 und 4, daher Zeitachse!
6
Statistik
Oder Balkendiagramm wenig erfreulich!
7
Statistik
Besser ... aus Platzersparnisgründen
hintereinander gestellt!.
8
Statistik
9
Statistik
Im 19. Jahrhundert galten statistische Daten
noch als unwissenschaftlich. Während es in der
Wissenschaft um Gewissheit ging, befasste sich
die Statistik mit Ungewissheit, und folglich war
die Statistik keine wissenschaftliche Methode im
eigentlichen Sinne. Die statistischen Studien
des ungarischen Arztes Ignaz Semmelweis bei
Kindbettfieber und Skorbut sind so legendär wie
die Weigerung der zuständigen Behörden, die
vorbeugenden Maßnahmen zu treffen, die seine
Statistiken nahe legten. Anders als in der Physik
setzte sich das statistische Denken bei der
medizinischen Diagnose und Therapie erst
allmählich durch. (Gigerenzer, S. 126)
Gerd Gigerenzer Das Einmaleins der Skepsis. Über
den richtigen Umgang mit Zahlen und Risiken.
Berlin Verlag 2002.
10
Statistik
Um die Früherkennung von Brustkrebs ab einem
bestimmten Alter zu fördern, wird Frauen
empfohlen, regelmäßig an Screenings (Reihentests
für Frauen ohne Symptome) teilzunehmen.
Angenommen, Sie führen in einer bestimmten Gegend
des Landes ein solches Brustkrebs-Screening mit
Hilfe von Mammographie durch. In der betreffenden
Gegend liegen folgende Angaben über Frauen
zwischen 40 und 50 vor, bei denen sich keine
Symptome zeigen und die am Mammographie-Screening
teilnehmen
Die Wahrscheinlichkeit, dass eine dieser Frauen
Brustkrebs hat, beträgt 0,8 Prozent. Wenn eine
Frau Brustkrebs hat, beträgt die
Wahrscheinlichkeit 90 Prozent, dass ihr
Mammogramm positiv ausfällt. Wenn eine Frau
jedoch keinen Brustkrebs hat, beträgt die
Wahrscheinlichkeit 7 Prozent, dass ihr Mammogramm
dennoch positiv ausfällt. Angenommen, bei einer
Frau ist das Mammogramm positiv. Wie hoch ist
die Wahrscheinlichkeit, dass sie tatsächlich
Brustkrebs hat.
(Gigerenzer, S. 65)
11
Statistik
Um die Früherkennung von Brustkrebs ab einem
bestimmten Alter zu fördern, wird Frauen
empfohlen, regelmäßig an Screenings (Reihentests
für Frauen ohne Symptome) teilzunehmen.
Angenommen, Sie führen in einer bestimmten Gegen
des Landes ein solches Brustkrebs-Screening mit
Hilfe von Mammographie durch. In der betreffenden
Gegend liegen folgende Angaben über Frauen
zwischen 40 und 50 vor, bei denen sich keine
Symptome zeigen und die am Mammographie-Screening
teilnehmen
Von jeweils 1 000 Frauen haben 8 Brustkrebs. Von
diesen 8 Frauen mit Brustkrebs werden 7 ein
positives Mammogramm haben. Von den übrigen 992
Frauen, die keinen Brustkrebs haben, werden rund
70 dennoch ein positives Mammogramm haben.
Stellen Sie sich nun eine Anzahl von Frauen vor,
deren Mammogramm beim Screening positiv ausfiel.
Wie viele von ihnen haben wirklich
Brustkrebs? (Gigerenzer, S. 65)
12
Brustkrebsrisiko
13
Darstellung der Bayesschen Regel
Bayessche Regel für natürliche Häufigkeiten
a ab
p (krank pos)
a Zahl der Personen, die positiv gestestet
wurden und erkrankt sind b Zahl der Personen,
die positiv gestestet wurden und nicht erkrankt
sind.
Bayessche Regel für bedingte Wahrscheinlichkeiten
p (krank) p (pos krank ) p (krank) p (pos
krank ) p (nicht krank) p (pos nicht krank )
p (krank pos)
14
Häufigkeiten versus Bedingte
Wahrscheinlichkeiten
15
Sensitivität und Spezifität
Sensitivität eines Tests (oder eines
Symptoms) Das ist die Wahrscheinlichkeit mit
der ein Kranker als krank erkannt wird.
Spezifität eines Tests (oder eines
Symptoms) Das ist die Wahrscheinlichkeit mit
der ein Gesunder als gesund erkannt
wird. Besser Die Wahrscheinlichkeit, mit der
bei Abwesenheit der Krankheit K das Symptom S
fehlt.
16
Prävalenz und Voraussagewerte
Prävalenz einer Erkrankung K eigentlich
relative Häufigkeit Das ist die
Wahrscheinlichkeit mit der ein Kranker als krank
erkannt wird.
Vorhersagewerte Prädikativer Wert des positiven
Befundes Prädikativer Wert des negativen
Befundes
17
Bayessche Formel
Bei einer Massenuntersuchung mit dem Test S wird
nach der Krankheit K gesucht. Annahme 1 Bei
Patienten, die an der Krankheit K leiden, spricht
der Test mit 99 Wahrscheinlichkeit positiv an,
d. h. Folglich hat der Test S die Sensitivität
0,99 .
Annahme 2 Insgesamt (also bei Gesunden und
Kranken zusammen genommen) ist der Test in 1
der Fälle positiv, d. h.
Frage Wie hoch ist die Wahrscheinlichkeit,
dass ein Patient an der Krankheit K erkrankt,
wenn der Test bei ihm positiv ist ?
18
Bayessche Formel
Lösung Berechne die Prävalenz
bezogen auf das Untersuchungsgut, in dem 1
der Tests positiv ist.
Fall 1 (Jeder Hundertste ist erkrankt.)
Fall 2 (Jeder Zehntausendste ist erkrankt.)
Zu Fall 1
Zu Fall 2
19
Bayessche Formel
Fall 1 (Jeder Hundertste ist erkrankt.)
Fall 2 (Jeder Zehntausendste ist erkrankt.)
In Fall 1 sind von 10 000 Personen 100 krank und
9 900 gesund. 100 Tests fallen positiv aus, dabei
werden 99 Kranke und ein Gesunder als krank
eingestuft. Also werden 9 899 Gesunde als gesund
eingestuft. Spezifität
In Fall 2 ist von 10 000 Personen nur einer krank
und 9 999 gesund. Falls er als krank eingestuft
würde, würden 99 der 9 999 Gesunden als krank
eingestuft. Spezifität
20
Bayessche Formel
Fall 1 und Fall 2 Gleiche Sensitivität (99) und
fast gleiche Spezifität (99,9 bzw. 99,0)
Aber Voraussagewerte eines positiven Resultats
unterscheiden sich sehr Fall 1 99, Fall 2
1. Das macht deutlich, wie wichtig die
Häufigkeiten der Krankheiten für die
Differentialdiagnose sind!
21
Sensitivität und Spezifität
Sensitivität und Spezifität eines Tests hängen
davon ab, wo die Grenze zwischen normal und
krankhaft gezogen wird. Welcher Laborwert ist
noch normal oder bereits pathologisch? Ist diese
Grenze einmal festgelegt, so liegen auch
Sensitivität und Spezifität fest! Der
Vorhersagewert hängt aber zusätzlich von der
Häufigkeit der Erkrankung im untersuchten
Kollektiv ab.
22
Vierfeldertafel
Tatsächliche Situation
Diagnose lautet aufgrund des Testergebnisses
Diagnostischer Voraussagewert (predictive
value)
krank (pos.) gesund (neg.)
Positiver Test, also krank!
richtig-positiv
falsch-positiv
A AB
A
B
D
C
D DC
Negativer Test, also gesund!
falsch-negativ
richtig-negativ
D
A
A
B
D
B
Spezifität
Sensitvität
23
Bayessche Forme bei unbekannter Häufigkeit des
Symptoms
In der Regel ist nicht die Wahrscheinlichkeit
P(S) für das Symptom S im untersuchten Kollektiv
bekannt. Meist sind bekannt die Prävalenz
P(K), die Sensitivität und die Spezifität
Daraus kann die Wahrscheinlichkeit P(S) berechnet
werden
Sensitivität Prävalenz
Das Symptom S kommt aber auch bei den nicht
erkrankten Personen im Kollektiv vor. Die
Spezifität gibt an, wie häufig S bei den nicht
erkrankten Personen fehlt, folglich ist 1
Spezifität der relative Anteil der nicht
erkrankten mit Symptom S.
24
Bayessche Forme bei unbekannter Häufigkeit des
Symptoms
Die Größe des nicht erkrankten Kollektivs ist
1-P(K) in diesem nicht erkrankten Teil des
Kollektivs kommt das Symptom S dann mit folgender
Häufigkeit vor (1-Spezifität)
(1-Prävlenz)
Durch Einsetzen in die Bayes-Formel ergibt sich
der positive Voraussagewert
Ähnlich ergibt sich der negative Voraussagewert
25
Screening auf Portiokarzinom

• Portioabstrich wird auf verdächtige Zellen
  durchgemustert.
• Zellen, die karzinomatös verändert aussehen
• gibt es bei Patientinnen, die ein Karzinom
  aufweisen (hier in größerer Zahl)
• gibt es bei Patientinnen, die kein Karzinom
  aufweisen.
• Frage Wo ist die Grenze ? Wann spricht der Arzt
  den Krebsverdacht aus?

• Wenn 1 verdächtiger Zellen die Grenze ist, wird
  man 95 der Karzinome erkennen.
  (Sensitivität 95, Fehler 2. Art 5)
• Andererseits werden nur 80 der karzinomfreien
  Patientinnen als gesund erkannt.
• (Spezifität 80, Fehler 1. Art 20)
• Legt man die Grenze auf 2 verdächtiger Zellen,
  so steigt die Spezifität von 80 auf 94,
  während die Sensitivität von 95 auf 78 fällt.

26
Strahlungs-induzierter Brustkrebs
27
Mammographie-Screenings in 58 australischen
Broschüren
28
Zahlen aus dem Krebsregister von Ontario, 1999
29
Sterblichkeit bei Krebsarten 1990 - 1995
30
Brustkrebsrisiko
31
Mit Hilfe des Hämokkulttests, mit dem man Blut im
Stuhl nachweist, lässt sich Darmkrebs
diagnostizieren. Dieser Test wird ab einem
bestimmten Alter durchgeführt, oft im Zuge eines
Screenings zur Früherkennung von Darmkrebs.
Angenommen, Sie führen in einer bestimmten Gegend
ein Hömokkulttest-Screening durch. Für über
50-jährige, symptomfreie Personen, die daran
teilnehmen, ist in der betreffenden Gegend
Folgendes bekannt
Die Wahrscheinlichkeit, dass ein Mitglied dieser
Population Darmkrebs hat, beträgt 0,3 Prozent.
Wenn eine Person Darmkrebs hat, beträgt die
Wahrscheinlichkeit 50 Prozent, dass der
Hämokkulttest positiv ausfällt. Wenn eine Person
keinen Darmkrebs hat, liegt die
Wahrscheinlichkeit, dass der Test dennoch positiv
ausfällt, bei 3 Prozent. Angenommen, bei einer
bestimmten Person (über 50 Jahre alt,
symptomfrei) ist das Testergebnis positiv. Mit
welcher Wahrscheinlichkeit hat sie wirklich
Darmkrebs? (Gigerenzer, S. 149)
32
Mit Hilfe des Hämokkulttests, mit dem man Blut im
Stuhl nachweist, lässt sich Darmkrebs
diagnostizieren. Dieser Test wird ab einem
bestimmten Alter durchgeführt, oft im Zuge eines
Screenings zur Früherkennung von Darmkrebs.
Angenommen, Sie führen in einer bestimmten Gegend
ein Hömokkulttest-Screening durch. Für über
50-jährige, symptomfreie Personen, die daran
teilnehmen, ist in der betreffenden Gegend
Folgendes bekannt
Von jeweils 10 000 Personen haben 30 Darmkrebs.
Bei 15 von diesen 30 Personen mit Krebs fällt der
Hämokkulttest positiv aus. Von den restlichen 9
970 Menschen ohne Darmkrebs fällt bei 300 der
Hämokkulttest dennoch positiv aus. Stellen Sie
sich eine gewisse Anzahl von Personen (über 50
Jahre alt, symptomfrei) vor, deren Hämokkulttest
positiv ausfiel. Wie viele von ihnen haben
wirklich Darmkrebs? (Gigerenzer, S. 149)
33
Brustkrebsrisiko
34
Darmkrebsrisiko
35
(No Transcript)
36
Mündliche Prüfungen Medizinische Methodologie,
Dr. Seising
Montag, 24. Januar 2005, Raum Bibliothek des IMC
09.00 Uhr
10.00 Uhr
11.00 Uhr
12.00 Uhr


14.00 Uhr
15.00 Uhr
16.00 Uhr
17.00 Uhr
37
Mündliche Prüfungen Medizinische Methodologie,
Dr. Seising
Dienstag, 25. Januar 2005, Raum Bibliothek des
IMC
09.00 Uhr
10.00 Uhr
11.00 Uhr
12.00 Uhr


14.00 Uhr
15.00 Uhr
16.00 Uhr
17.00 Uhr
38
Mündliche Prüfungen Medizinische Methodologie,
Dr. Seising
Mittwoch, 26. Januar 2005, Raum Bibliothek des
IMC
09.00 Uhr
10.00 Uhr
11.00 Uhr
12.00 Uhr


14.00 Uhr
15.00 Uhr
16.00 Uhr
17.00 Uhr