Inductive Reasoning

1
Inductive Reasoning
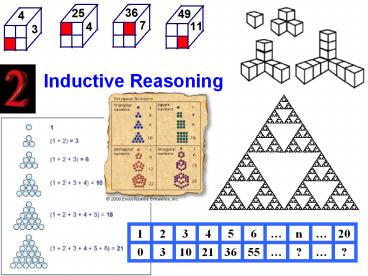
1 2 3 4 5 6 n 20
0 3 10 21 36 55 ? ?
2
Quadratic Sequences
Terms 4, 25, 36, 49, 64
3, 24, 35, 48, 63 6, 12, 20, 30, 42
3
Factorable Quadratic Sequences
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
6
8
12
14
No common Gap !
10
2
2
2
2
This sequence is no longer linear. It is
not constant till the 2nd level. It is quadratic
as can seen in the graph of the points.
4
As you can see, this graph is part of a
parabola or quadratic equation.
If we examine some characteristics of
quadratic equations, we will be able to see how
these equations can be converted into two linear
sequences for which it is very easy to find
formulas.
5
Solving Quadratic Equations
Set to 0, then factor.
Wait !

The two factors are in y mx b form.
If we factor the terms into linear
sequences, then each factor can be easily
converted into an algebraic expression in the
form or mx b.
6
Break terms into factors
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
16
120
112
23
26
210
34
45
6
8
12
14
10
2
2
2
2
Only certain combination will create two
linear sequences. Our difficulty is determining
which factors will create the sequences.
7
Do you see the pattern ?
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
16
120
112
78
56
67
23
26
210
34
45
6
8
12
14
10
2
2
2
2
It does !
Lets see if the pattern continues.
8
Now find the formula for the green sequence.
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
(x 1)
78
56
67
23
34
45
6
8
12
14
10
2
2
2
2
For the green sequence, the gap between
terms is 1. Therefore the slope is 1.
2 (1)1 b
1 b
(x 1)
9
Now find the formula for the red sequence.
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
(x 1)
78
(x 2)
56
67
23
34
45
6
8
12
14
10
2
2
2
2
For the red sequence, the gap between terms
is also 1. Therefore the slope is 1.
3 (1)1 b
2 b
(x 2)
10
Now lets find the 20th term.
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
(x 1)
78
(x 2)
56
67
23
34
45
6
8
12
14
10
2
2
2
2
(x 2)
(x 1)
Substitute 20 for x.
462
(21)(22)
11
Lets try another problem.
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 55
...
7
9
13
15
11
2
2
2
2
12
Factor the terms
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 55
...
116
127
17
Skip Too many
26
28
39
34
44
7
9
13
15
11
2
2
2
2
Do you see the pattern?
13
Test to see if it really works.
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 55
...
17
Skip Too many
511
28
39
410
7
9
13
15
11
2
2
2
2
It really does work.
14
Now find the formula for the green sequence.
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 72
...
(x-1)
17
Skip Too many
511
28
39
410
7
9
13
15
11
2
2
2
2
For the green sequence, the gap between
terms is 1. Therefore the slope is 1.
(x-1)
1 (1)2 b
-1 b
15
Now find the formula for the red sequence.
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 72
...
(x-1)
17
Skip Too many
511
28
39
410
(x 5)
7
9
13
15
11
2
2
2
2
For the red sequence, the gap between terms
is 1. Therefore the slope is 1.
7 (1)2 b
5 b
(x 5)
16
Lets find the 20th term
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 72
...
(x-1)
17
Skip Too many
511
28
39
410
(x 5)
7
9
13
15
11
2
2
2
2
(x-1)(x 5)
475
(19)(25)
17
Elimination Strategies
All linear sequence either constantly increase or
constantly decrease.
Therefore if the sequence doesnt continually
increase or decrease, the factors can be
rejected.
Knowing this will increase the speed of finding
the correct set of factors..
18
Revisit first problem.
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
16
112
23
26
34
6
8
12
14
10
2
2
2
2
1 12 can be immediately rejected because the
green factors do not change.
2 6 can be immediately rejected because either
way the green factors do not change or the red
factors do not change .
19
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
16
112
23
26
34
45
56
67
6
8
12
14
10
2
2
2
2
Doesnt work because the values do not increase
in the red factors.
20
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
16
112
23
26
34
6
8
12
14
10
2
2
2
2
Applying the pattern of increasing each factor by
1 each time, we can predict the next factor terms.
21
Note that now we did not need to try as many
factor combinations.
x 1 2 3 4 5 6 x ...
20
y 6 12 20 30 42 56
...
16
112
23
26
34
45
56
67
6
8
12
14
10
2
2
2
2
Now it is easy to compute the linear formula
for each factor sequence.
22
By using the concept that the linear factors
need to increase or decrease every time, the
number of trials to find the correct sequence of
factors is greatly reduced.
23
Revisit second problem.
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 72
...
116
17
Skip Too many
26
28
34
44
7
9
13
15
11
2
2
2
2
1 16 can be immediately rejected because the
green factors do not change.
4 4 can be immediately rejected because either
way the green factors do not change or the red
factors do not change properly.
24
Revisit second problem.
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 55
...
116
17
Skip Too many
26
28
39
410
511
34
44
7
9
13
15
11
2
2
2
2
The pattern is quickly discovered. Therefore the
next factors can be predicted and tested.
25
Revisit second problem.
x 1 2 3 4 5 6 x ...
20
y 0 7 16 27 40 55
...
116
17
Skip Too many
26
28
39
410
511
34
44
7
9
13
15
11
2
2
2
2
The pattern works. Now we could compute the
linear formulas for each factor sequence. But we
will not at this time.
26
Now we need to practice.
Lets begin.
27
Practice 1a
x 1 2 3 4 5 6 x ...
20
y 0 5 12 21 32 45
...
5
7
11
13
9
2
2
2
2
Factor each term.
28
Practice 1b
x 1 2 3 4 5 6 x ...
20
y 0 5 12 21 32 45
...
112
15
Skip Too many
26
26
34
34
5
7
11
13
9
2
2
2
2
1 12 can be immediately rejected because the
green factors do not change.
3 4 can be immediately rejected because either
way the green factors do not change or the red
factors do not change .
29
Practice 1c
x 1 2 3 4 5 6 x ...
20
y 0 5 12 21 32 45
...
112
15
Skip Too many
26
26
37
48
59
34
34
5
7
11
13
9
2
2
2
2
It really does works.
The pattern is quickly discovered. Therefore the
next factors can be predicted and tested.
30
Practice 1d
x 1 2 3 4 5 6 x ...
20
y 0 5 12 21 32 45
...
(x-1)
15
Skip Too many
26
37
48
59
5
7
11
13
9
2
2
2
2
For the green sequence, the gap between
terms is 1. Therefore the slope is 1.
(x-1)
1 (1)2 b
-1 b
31
Practice 1e
x 1 2 3 4 5 6 x ...
20
y 0 5 12 21 32 45
...
(x-1)
15
Skip Too many
26
37
(x 3)
48
59
5
7
11
13
9
2
2
2
2
For the red sequence, the gap between terms
is 1. Therefore the slope is 1.
(x 3)
5 (1)2 b
3 b
32
Practice 1f
x 1 2 3 4 5 6 x ...
20
437
y 0 5 12 21 32 45
...
(x-1)
15
Skip Too many
26
37
(x 3)
48
59
5
7
11
13
9
2
2
2
2
Lets find the 20th term
(x 3)
(x-1)
437
(19) (23)
33
Practice 2a
x 1 2 3 4 5 6 x ...
20
y 18 28 40 54 70 88
...
10
12
16
18
14
2
2
2
2
Factor each term.
34
Practice 2b
x 1 2 3 4 5 6 x ...
20
y 18 28 40 54 70 88
...
128
118
214
29
58
69
710
811
47
36
10
12
16
18
14
2
2
2
2
1 28 can be immediately rejected because the
green factors do not change.
2 14 can be immediately rejected because either
way the green factors do not change or the red
factors do not change .
35
Practice 2c
x 1 2 3 4 5 6 x ...
20
y 18 28 40 54 70 88
...
128
118
214
29
58
69
710
811
47
36
10
12
16
18
14
2
2
2
2
It really does works.
The pattern is quickly discovered. Therefore the
next factors can be predicted and tested.
36
Practice 2d
x 1 2 3 4 5 6 x ...
20
y 18 28 40 54 70 88
...
(x 2)
58
69
710
811
47
36
10
12
16
18
14
2
2
2
2
For the green sequence, the gap between
terms is 1. Therefore the slope is 1.
(x 2)
3 (1)1 b
2 b
37
Practice 2e
x 1 2 3 4 5 6 x ...
20
y 18 28 40 54 70 88
...
(x 2)
(x 5)
58
69
710
811
47
36
10
12
16
18
14
2
2
2
2
For the red sequence, the gap between terms
is 1. Therefore the slope is 1.
(x 5)
6 (1)1 b
5 b
38
Practice 2f
x 1 2 3 4 5 6 x ...
20
550
y 18 28 40 54 70 88
...
(x2)
(x 5)
58
69
710
811
47
36
10
12
16
18
14
2
2
2
2
Lets find the 20th term
(x 5)
(x2)
550
(22) (25)
39
Practice 3a
x 1 2 3 4 5 6 x ...
20
y 20 30 42 56 72 90
...
10
12
16
18
14
2
2
2
2
Factor each term.
40
Practice 3b
x 1 2 3 4 5 6 x ...
20
y 20 30 42 56 72 90
...
130
120
215
210
45
10
12
16
18
14
2
2
2
2
1 30 can be immediately rejected because the
green factors do not change.
2 15 can be immediately rejected because either
way the green factors do not change or the red
factors do not change .
41
Practice 3c
x 1 2 3 4 5 6 x ...
20
y 20 30 42 56 72 90
...
17
120
215
210
310
45
512
10
12
16
18
14
2
2
2
2
3 10 can be immediately rejected because either
way the green factors do not change or the red
factors do not change .
42
Practice 3d
x 1 2 3 4 5 6 x ...
20
y 20 30 42 56 72 90
...
17
120
215
210
67
78
89
910
310
45
56
10
12
16
18
14
2
2
2
2
It really does works.
The pattern is quickly discovered. Therefore the
next factors can be predicted and tested.
43
Practice 3e
x 1 2 3 4 5 6 x ...
20
y 20 30 42 56 72 90
...
(x 3)
67
78
89
910
45
56
10
12
16
18
14
2
2
2
2
For the green sequence, the gap between
terms is 1. Therefore the slope is 1.
(x 3)
4 (1)1 b
3 b
44
Practice 3f
x 1 2 3 4 5 6 x ...
20
y 20 30 42 56 72 90
...
(x 3)
67
78
89
910
(x 4)
45
56
10
12
16
18
14
2
2
2
2
For the red sequence, the gap between terms
is 1. Therefore the slope is 1.
(x 4)
5 (1)1 b
4 b
45
Practice 3g
x 1 2 3 4 5 6 x ...
20
552
y 20 30 42 56 72 90
...
(x 3)
67
78
89
910
(x 4)
45
56
10
12
16
18
14
2
2
2
2
Lets find the 20th term
(x 3)
(x 4)
552
(23) (24)
46
Practice 4a
x 1 2 3 4 5 6 x ...
20
y 0 9 20 33 48 65
...
Skip Too many
9
11
15
17
13
2
2
2
2
Factor each term.
47
Practice 4b
x 1 2 3 4 5 6 x ...
20
y 0 9 20 33 48 65
...
120
19
Skip Too many
33
210
45
9
11
15
17
13
2
2
2
2
1 20 can be immediately rejected because the
green factors do not change.
Lets try the pattern of 19 and 210.
48
Practice 4c
x 1 2 3 4 5 6 x ...
20
y 0 9 20 33 48 65
...
120
19
Skip Too many
33
210
311
412
513
45
9
11
15
17
13
2
2
2
2
It really works.
First try is a charm.
49
Practice 4d
x 1 2 3 4 5 6 x ...
20
y 0 9 20 33 48 65
...
(x - 1)
19
Skip Too many
210
311
412
513
9
11
15
17
13
2
2
2
2
For the green sequence, the gap between
terms is 1. Therefore the slope is 1.
(x - 1)
1 (1)2 b
-1 b
50
Practice 4e
x 1 2 3 4 5 6 x ...
20
y 0 9 20 33 48 65
...
(x - 1)
19
Skip Too many
210
311
(x 7)
412
513
9
11
15
17
13
2
2
2
2
For the red sequence, the gap between terms
is 1. Therefore the slope is 1.
(x 7)
9 (1)2 b
7 b
51
Practice 4f
x 1 2 3 4 5 6 x ...
20
513
y 0 9 20 33 48 65
...
(x - 1)
19
Skip Too many
210
311
(x 7)
412
513
9
11
15
17
13
2
2
2
2
Lets find the 20th term
(x 7)
(x - 1)
513
(19) (27)
52
Summary
When the gap between terms of sequences are
constant on the second level, the sequence is
quadratic or second degree.
The rule for each term is created by the
factors of each term which create their own
linear sequence.
The quadratic sequence is treated as the
product of 2 linear sequences.
53
Time can be saved by assuming a pattern
exists in the first two columns of factors, then
seeing if the terms can correctly predict the
following terms.
Also, time can be saved by rejecting terms
that do not increase or decrease.
These problems require a lot of practice.
54
Cest fini.
Good day and good luck.
Thats all folks.
A Senior Citizen Production
55
Cest fini.
Good day and good luck.