Reverse correlation and visual receptive fields - PowerPoint PPT Presentation
1 / 34
Title:
Reverse correlation and visual receptive fields
Description:
1. PINZELLADES D'ANATOMIA I FISIOLOGIA EL CERVELL Divisi funcional Divisi anat mica CERVELL L bul parietal L bul frontal L bul occipital L bul temporal – PowerPoint PPT presentation
Number of Views:72
Avg rating:3.0/5.0
Title: Reverse correlation and visual receptive fields
1
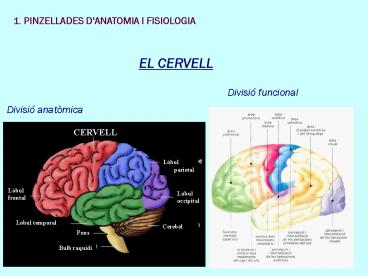
1. PINZELLADES D'ANATOMIA I FISIOLOGIA
EL CERVELL
Divisió funcional
Divisió anatòmica
2
1. PINZELLADES D'ANATOMIA I FISIOLOGIA
LES NEURONES
Parts principals
Tipus de neurones
3
PINZELLADES D'ANATOMIA I FISIOLOGIA
LA MEMBRANA CELULAR
- Actua com una CAPACITÀNCIA,
- impermeable a molècules carregades.
Cm dV/dtIapp,
(Vpotencial de la membrana, Iappintensitat del
corrent Cmcapacitància de la membrana)
- Els canals són selectius als tipus
- d'ions (K,Na,...)
4
PINZELLADES D'ANATOMIA I FISIOLOGIA
IMPULS NERVIÓS MECANISMES DINTERCANVI IÒNIC
- Atracció elèctrica
- En repòs, càrrega negativa a linterior de la
cèl.lula - (dif. de potencial d'uns 70mV).
- Convenció el potencial del fluid extracel.lular
val 0 - Difusió a través de canals deguda a les dif. de
concentració - Concentracions de Na i Ca2 més altes fora
(entren per difusió) - Concentracions de K més altes dintre (surten
per difusió) - Bombeig d'ions (requereix energia)
5
PINZELLADES D'ANATOMIA I FISIOLOGIA
L'IMPULS NERVIÓS
6
PINZELLADES DANATOMIA I FISIOLOGIA
CAP ENDINS O CAP ENFORA?POTENCIAL DEQUILIBRI i
POTENCIAL REVERS
Potencial dequil.libriEquil.libri entre el flux
degut a forces elèctriques i el difusiu. Per a
canals monoiònics... EVT/z log(ext/int),
(Eq. de Nernst) on VTkB T/q znúmero de
protons qcàrrega d1 ió kBconstant de
Boltzmann Ttemperatura ext, int
concentracions Exemples (mV). EK?(-90,-70),
ENa gt 50, ECa2150
7
PINZELLADES DANATOMIA I FISIOLOGIA
POTENCIAL REVERS
Per a canals menys selectius, i depenent de la
permeabilitat relativa de cada tipus dió,
lequació de Goldman (mitjana ponderada) dóna el
potencial revers (VR). Per norma general, el
potencial en repòs duna neurona és duns -65mV
8
PINZELLADES DANATOMIA I FISIOLOGIA
EQUACIÓ BÀSICA PER AL POTENCIAL DE LA MEMBRANA,
v(t)
Cm dv/dt - im Iapp -Si gi (v-Ei)Iapp
gi conductàncies gt 0
Iapp corrents aplicats (electrodes,...)
im corrents iònics
Cm capacitància, normalment constant
9
2. EQUACIONS DIFERENCIALS CLÀSSIQUES DE
LACTIVITAT NEURONAL
LEQUACIÓ DEL CABLE
El potencial de la membrana pot no ser uniforme
al llarg de laxó
VV(x,t)
10
EQ. DIFERENCIALS "CLÀSSIQUES" DE L'ACTIVITAT
NEURONAL
LEQUACIÓ DEL CABLE
SIMPLIFICACIONS PER AL TRACTAMENT ANALÍTIC
- TEORIA DEL CABLE LINEAL
- Ignorar corrents iònics im(V-Vrepòs )/rm
- a(x)a
- CABLE INFINIT
- MODEL DE ROLL (SOMA-DENDRITA)
- MODELS COMPARTIMENTALS
- Neurones electrotònicament compactes.
11
Estudi dels corrents iònics el model de
Hodgkin-Huxley (1952)
EQUACIONS DIFERENCIALS DE LACTIVITAT NEURONAL
Tècniques d emmordassament (clampatge)
desenvolupades del 1939 al 1949, aprox.
El pobre calamar NO va rebre cap premi... No
sabem si va acabar a la romana o farcit!
AL Hodgkin i AF Huxley (conjuntament amb JC
Eccles per sinapsis en neurones motores) van
rebre el Premi Nobel de Fisiologia i Medicina el
1963.
12
Estudi dels corrents iònics el model de
Hodgkin-Huxley (1952)
EQUACIONS DIFERENCIALS DE LACTIVITAT NEURONAL
(considerem neurones electrotònicament compactes,
vv(t))
Variables comporta
PNamk h PKns k3, s4 típicament
13
Time constants for the gating variables
Steady state curves for the gating variables
v (mV)
v (mV)
h
n
14
El model de Hodgkin-Huxley (1952), per a
neurones electrotònicament compactes, vv(t)
EQUACIONS DIFERENCIALS DE LACTIVITAT NEURONAL
Les conductàncies depenen de les variables
comporta
15
EQUACIONS DIFERENCIALS DE LACTIVITAT NEURONAL
Mesures obtingudes (usant mètodes de regressió)
per Hodgkin, Huxley i col.laboradors
unitat ms-1
CONDUCTÀNCIES gL0.3, gNa120, gK36
(mS/cm2) POTENCIALS REVERSOS VL10.6,
VNa115, VK-12 (mV) CAPACITÀNCIA C1
(µF/cm2), Iapp (µA/cm2)
Contínuament sestan mesurant noves cèl.lules
(diferents animals, diferents parts del sistema
nerviós), que situen el problema en espais de
paràmetres nous i, per tant, davant de
comportaments qualitatius de les EDOs
eventualment diferents.
16
EQUACIONS DIFERENCIALS DE LACTIVITAT NEURONAL
Other models
Hodgkin-Huxley equations are the paradigm of
model of neuron, but for some purposes
(integrability, numerical treatment, analytical
treatment,...) more simplified models are often
used.
Explicit equation of conductances
Cm dv/dt - gL (v -VL) - gk (v -Vk) Iapp dgk
/dt e (Gk(v) -gk)
17
EQUACIONS DIFERENCIALS DE LACTIVITAT NEURONAL
Membrane potential of an IF neuron
Reprinted from Dayan Abbott, Theoretical
neuroscience
18
3. Altres matemàtiques de la neurociència
Aplicació retinotòpica
polars e, a
cartesianes x, y
X l ln(1 e/e0), Y - l e a p / (e0 e) /180
Quan egtgt1o, ens dóna el logaritme complex
19
Percepció
aplicació retinotòpica
20
Percepció
aplicació retinotòpica
21
Model neurona a neurona del còrtex visual
primari
DW McLaughlin, M Shapley, R Shelley, J Wielaard A
neuron network model of macaque primary visual
cortex (V1) orientation selectivity and dynamics
in the input layer 4Ca Proceedings National
Academy of Sciences (2000) 97 8087-8092.
Construeixen un model de 16384 equacions
diferencials que modela 1mm2 del córtex visual
primari (hi ha, a més, una simetria important en
el CVP). Tenen en compte tots els coneixements
anatòmics i fisiològics del moment, reprodueixen
fenòmens ja coneguts i potencialment poden donar
respostes a preguntes on lexperimentació no pot
arribar. El model està en fase de millora,
intentant aconseguir que la proporció de
cèl.lules simples i complexes sadigui amb la
hipòtesi que manegen els fisiòlegs. Tot i així,
es mostra robust quant als seus resultats
inicials.
22
xi j centre del camp receptiu d1 neurona de
lLGN x coord. pla visual escollides
aleatòriam. A diferència de Gaussianes, nuclis
espacials GLGN nuclis temporals de lLGN
dintegral zero
Conductàncies gEEj(t) FEESEE Sk aj,k Sl
GE(t-tlk), gEIj(t) fEI0(t)SEI Sk bj,k Sl
GI(t-Tlk)
- 1 mm2 de 4Ca
- 21416384 neurones al model
- aprox. 20000 real.
Equacions principals dvPj/dt - l vPj - gPEj(t)
(vPj- VE) - gPIj(t) (vPj-VI)
23
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Cor
relació reversa i camps receptius visuals
Objectiu estimar taxes d'impulsos r(t) evocades
per un estímul arbitrari s(t) i.e., com
reaccionarà una cèl.lula davant d'un determinat
estímul?
CÈL.LULA
MÓN VISUAL
s(t)
t
resposta
estímul
24
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Cor
relació reversa i camps receptius visuals
- Només estimacions lineals de la resposta.
- Especialment vàlid en les primeres etapes del
recorregut visual - No es tenen en compte sinapsis als circuits
interns
pes
activitat de fons
Hipòtesi addicional avaluem només fluctuacions
al voltant de la mitjana
Un incís...
25
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Cor
relació reversa i camps receptius visuals
és una linealització d'una sèrie de Volterra
Existeix un reordenament degut a Wiener d'aquí
que D sanomeni nucli de Wiener
tornem a lexplicació...
26
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Nuc
lis de Wiener òptims
D ha de minimitzar
Derivant funcionalment respecte D tenim que
Correlació reversa
on
són funcions de correlació
27
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Nuc
lis de Wiener òptims
Lequació
es pot resoldre per transformacions de Fourier, i
sobté
- Exemple quan lestímul és soroll blanc,
- es pot integrar explícitament.
28
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA No
linealitat
- Les neurones i el sistema nerviós són no
lineals!! - Actualment, es duen a terme estimacions de l'estil
(F habitualment sigmoidals, Th. Busgang per a
soroll blanc,...)
29
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Cam
ps receptius visuals
Les neurones de la retina, lLGN i el còrtex
visual primari responen a estímuls visuals en
zones concretes del camp visual anomenades camps
receptius. El problema rau en conèixer
lestructura temporal i espacial daquests camps.
També poden rebre alguns efectes indirectes
externs al camp receptiu (per exemple, inhibició
lateral, però aquest és un altre problema
d'investigació molt obert -Adelson,...-)
30
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Càl
cul de camps receptius (neurones del CVP).
Volem estudiar el camp receptiu d'una neurona. A
la part lineal de rest(t) hi hauríem dafegir
ara les variables x,y. Lestimació lineal de
r(t), aleshores, sescriuria com
D(x,y,t) determina la força amb què un estímul a
(x,y) a linstant t-t afecta la taxa d'impulsos
de la neurona a linstant t
- Exemple quan lestímul és soroll blanc, sabem
que
Fem la separació de variables D(x,y,t) Ds(x,y)
Dt(t) (si observem que lestructura espacial
del camp receptiu és objecte, com a molt,
dhomotècies al variar el temps)
31
CODIFICACIÓ NEURONAL RELACIÓ ESTÍMUL-RESPOSTA Càl
cul de camps receptius (neurones del CVP).
Gràfiques Maple
D(x,y,t) Ds(x,y) Dt(t)
Experimentant i aproximant les dades per funcions
elementals, sobtenen les següents funcions per a
neurones del còrtex visual primari (CVP).
Funcions de Gabor espacials
Funcions de Gabor temporals
Zones ON/OFF d'un camp receptiu, i combinació amb
estímuls descombrat.
32
Desplegament de cervells
B Fischl, MI Sereno, AM Dale Cortical
surface-based analysis. II Inflation,
flattening, and a surface-based coordinate
system. Neuroimage (1999) 9(2)195-207
La superfície de lescorça cerebral humana és un
full amb molts plegaments. La major part de la
seva superfície roman enterrada entre aquests
plegaments. Amb això, es converteix en un camp
difícil per a la computació així com per a la
visualització. Els autors han dissenyat un
conjunt de procediments per modificar la
representació de la superfície cortical per tal
de (i) inflar-la de manera que lactivitat
enterrada en els solcs es pugui visualitzar,
(ii) tallar i aplanar un hemisferi sencer, i
(iii) transformar un hemisferi en una
superfice parametrtizable simple com ara una
esfera amb lobjectiu destablir un sistema de
coordenades basat a la superfície.
33
Altres temes
- Filtratges de senyals convolucions, FFT.
- Quina quantificació de l'estímul dóna una
resposta neuronal? - Teoria de la informació (entropia i informació
mútua). - Relació resposta-estímul distribucions de
Poisson. - Aprenentatge xarxes neuronals, supervisades o
no. - Models d'atenció, memòria, aprenentatge,... que
involucren - diferents àrees cerebrals. acoblament de
poblacions HH amb - característiques diferents.
34
Bibliografia
- P. Dayan, L.F. Abbott.
- Theoretical neuroscience. MIT pres, 2001
- C. Koch.
- Biophysics of computation. Oxford University
Pres, 1999 - J. Keener, J. Sneyd.
- Mathematical physiology. Springer-Verlag, 1998
- M.F. Bear, B.W. Connors, M.A. Paradiso.
- Neuroscience. Exploring the brain. Williams
Wilkins, 1996 - D.H. Hubel.
- Eye, brain and vision. Scientific American
Library, 1988.