Kapitel 4 / 1 - PowerPoint PPT Presentation
1 / 42
Title:
Kapitel 4 / 1
Description:
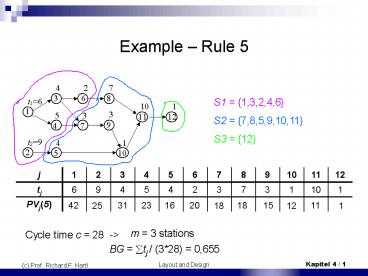
Example Rule 5 S1 = {1,3,2,4,6} S2 = {7,8,5,9,10,11} S3 = {12} j 1 2 3 4 5 6 7 8 9 10 11 12 tj 6 9 4 5 4 2 3 7 3 1 10 1 PVj(5) 42 31 23 16 20 18 11 15 25 18 1 12 ... – PowerPoint PPT presentation
Number of Views:93
Avg rating:3.0/5.0
Title: Kapitel 4 / 1
1
Example Rule 5
S1 1,3,2,4,6 S2 7,8,5,9,10,11 S3 12
j 1 2 3 4 5 6 7 8 9 10 11 12
tj 6 9 4 5 4 2 3 7 3 1 10 1
PVj(5)
42
31
23
16
20
18
11
15
25
18
1
12
m 3 stations
Cycle time c 28 -gt
BG ?tj / (328) 0,655
2
Example Regel 7, 6 und 2
- 3
j 1 2 3 4 5 6 7 8 9 10 11 12
PVj(7)
PVj(6)
PVj(2)
1
2
1
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
2
2
2
1
1
10
3
2
6
9
4
5
4
3
7
Apply rule 7 (latest possible station) at
first If this leads to equally prioritized
operatios -gt apply rule 6 (minimum number of
stations for j and all predecessors) If this
leads to equally prioritized operatios -gt appyl
rule 2 (decreasing processing times tj)
Solution c 28 ? m 2 BG 0,982 S1
1,3,2,4,5 S2 7,9,6,8,10,11,12
3
More heuristic methods
- Stochastic elements for rules 2 to 7
- Random selection of the next operation (out of
the set of operations ready to be applied) - Selection probabilities proportional or
reciprocally proportional to the priority value - Randomly chosen priority rule
- Enumerative heuristics
- Determination of the set of all feasible
assignments for the first station - Choose the assignment leading to the minimum idle
time - Proceed the same way with the next station, and
so on (greedy)
4
Further heuristic methods
- Heuristics for cuttingpacking problems
- Precedence conditions have to be considered as
well - E.g. generalization of first-fit-decreasing
heuristic for the bin packing problem. - Shortest-path-problem with exponential number of
nodes - Exchange methods
- Exchange of operations between stations
- Objective improvement in terms of the
subordinate objective of equally utilized stations
5
Worst-Case analysis of heuristics
- Solution characteristics for integer c and tj
- (j 1,...,n) for alternative 2
- ? Total workload of 2 neigboured stations has to
exceed the cycle time - Worst-Case bounds for the deviation of a solution
with m - Stations from a solution with m stations
m/m ? 2 - 2/m for even m and m/m ? 2 - 1/m
for odd m m lt c?m/(c - tmax 1) 1
6
Determination of cyle time c
- Given number of stations
- Cycle time unknown
- Minimize cycle time (alternative 1) or
- Optimize cycle time together with the number of
stations trying to maximize the systems
efficiency (alternative 3).
7
Iterative approach for determination of minimal
cycle time
- Calculate the theoretical minimal cycle
time(or cmin tmax if this is larger) and
c cmin - Find an optimal solution for c with minimum m(c)
by applying methods presented for alternative 1 - If m(c) is larger than the given number of
stations increase c by ? (integer value) and
repeat step 2.
8
Iterative approach for determination of minimal
cycle time
- Repeat until feasible solution with cycle time ?
c and number of stations ? m is found - If ? gt 1, an interval reduction can be applied
if for c a solution with number of stations ? m
has been found and for c-? not, one can try to
find a solution for c-?/2 and so on
9
Example rule 5
- m 5 stations
- Find maximum production rate, i.e. minimum
cycle time
j 1 2 3 4 5 6 7 8 9 10 11 12
tj 6 9 4 5 4 2 3 7 3 1 10 1
PVj(5) 42 25 31 23 16 20 18 18 15 12 11 1
cmin ?tj/m 55/5 11 (11 gt tmax 10)
10
Example rule 5
- Solution c 11
- 1,3, 2,6, 4,7,9, 8,5, 10,11, 12
- Needed 6 gt m 5 stations
- ? c 12, assign operation 12 to station 5
- ? S5 10,11,12
For larger problems usually, c leading to an
assignment for the given number of stations, is
much larger than cmin. Thus, stepwise increase of
c by 1 would be too time consuming -gt increase by
? gt 1 is recommended.
11
Classification of complex line balancing problems
- Parameters
- Number of products
- Assignment restrictions
- Parallel stations
- Equipment of stations
- Station boundaries
- Starting rate
- Connection between items and transportation
system - Different technologies
- Objectives
12
Number of products
- Single-product-models
- 1 homogenuous product on 1 assembly line
- Mass production, serial production
- Multi-product models
- Combined manufacturing of several products on 1
(or more) lines. - Mixed-model-assembly Products are variations
(models) of a basic product ? they are processed
in mixed sequence - Lot-wise multiple-model-production Set-up
between production of different products is
necessary ? Production lots (the line is
balanced for each product separately) ?
Lotsizing and scheduling of products ? TSP
13
Assignment restrictions
- Restricted utilities
- Stations have to be equipped with an adequate
quantity of utilities - Given environmental conditions
- Positions
- Given positions of items within a station? some
operation may not be performed then (e.g.
underfloor operations) - Operations
- Minimum or maximum distances between 2 operations
(concerning time or space) - ? 2 operations may not be assigned to the same
station - Qualifications
- Combination of operations with similiar complexity
14
Parallel stations
- Models without parallel stations
- Heterogenuous stations with different operations
? serial line - Models with parallel stations
- At least 2 stations performing the same operation
- Alternating processing of 2 subsequent operations
in parallel stations - Hybridization Parallelization of operations
- Assignment of an operation to 2 different
stations of a serial line
15
Equipment of stations
- 1-worker per station
- Multiple workers per station
- Different workloads between stations are possible
- Short-term capacity adaptions by using jumpers
- Fully automated stations
- Workers are used for inspection of processes
- Workers are usually assigned to several stations
16
Station boundaries
- Closed stations
- Expansion of station is limited
- Workers are not allowed to leave the station
during processing - Open stations
- Workers my leave their station in (rechtsoffen)
or in reversed (linksoffen) flow direction of
the line - Short-term capacity adaption by under- and
over-usage of cycle time. - E.g. Manufacturing of variations of products
17
Starting rate
- Models with fixed statrting rate
- Subsequent items enter the line after a fixed
time span. - Models with variable starting rate
- An item enters the line once the first station of
the line is idle - Distances between items on the line may vary (in
case of multiple-product-production)
18
Connection between items and transportation
systems
- Unmoveable items
- Items are attached to the transportation system
and may not be removed - Maybe turning moves are possible
- Moveable items
- Removing items from the transportation system
during processing is - Post-production
- Intermediate inventories
- Flow shop production without fixed time
constraints for each station
19
Different technologies
- Given production technologies
- Schedules are given
- Different technologies
- Production technology is to be chosen
- Different alternative schedules are given
(precedence graph) and/or - different processing times for 1 operation
20
Objectives
- Time-oriented objectives
- Minimization of total cycle time, total idle
time, ratio of idle time, total waiting time - Maximization of capacity utilization (systems
efficieny) most relevant for (single-product)
problems - Equally utilized stations
- Further objectives
- Minimization of number of stations in case of
given cycle time - Minimization of cycle time in case of given
number of stations - Minimization of sum of weighted cycle time and
weighted number of stations
21
Objectives
- Profit-oriented approaches
- Maximization of total marginal return
- Minimization of total costs
- Machines- and utility costs (hourly wage rate of
machines depends on the number of stations) - Labour costs often identical rates of labour
costs for all workers in all stations) - Material costs defined by output quantity and
cycle time - Idle time costs Opportunity costs depend on
cycle time and number of stations
22
Multiple-product-problems
- Mixed model assemblySeveral variants of a basic
product are processed in mixed sequence on a
production line. - Processing times of operations may vary between
the models - Some operations may not be necessary for all of
the variants - ? Determination of an optimal line balancing and
of an optimal sequence of models.
23
- multi-model
- Lot-wisemixed-model
- production
- With machine set-up
24
- mixed-model
- Without set-up
- Balancing for a theoretical average model
25
Balancing mixed-model assembly lines
- Similiar models
- Avoid set-ups and lot sizing
- Consider all models simultaneously
- Generalization of the basic model
- Production of p models of 1 basic model with up
to n operations production method is given - Given precedence conditions for operations in
each model j 1,...,n ? aggregated precendence
graph for all models - Each operation is assigned to exactly 1 station
- Given processing times tjv for each operation j
in each model v - Given demand bv for each model v
- Given total time T of the working shifts in the
planning horizon
26
Balancing mixed-model assembly lines
- Total demand for all models in planning horizon
- Cumulated processing time of operation j over
all models in planning horizon
27
LP-Model
- Aggregated model
- Line is balanced according to total time T of
working shifts in the planning horizon. - Same LP as for the 1-product problem, but cycle
time c is replaced by total time T
28
LP-Model
- Objective function
number of the last station (job n)
Constraints for all j 1, ... , n ... Each
job in 1 station for all k 1, ... , ...
Total workload in station k for all ...
Precedence conditions for all j and k
29
Example
v 1, b1 4 v 2, b2 2
v 3, b3 1 aggregated model
30
Example
- Applying exact method
- given T 70
- Assignment of jobs to stations with m 7
stationsS1 1,3S2 2 S3 4,6,7 S4
8,9 S5 5,10 S6 11 S7 12
31
Parameters
- ... Workload of station k for model v in T
- ... Average workload of m stations for model v
in T - Per unit
- ... Workload of station k for 1 unit of
model v - ... Avg. workload of m stations for 1 unit of
model v - Aggregated over all models
- ... Total workload of station k in T
32
Example parameters per unit
?kv Station k Avg.
Model v 1 2 3 4 5 6 7 ?v
1 10 7 11 10 6 10 1 7,86
2
3
x 4
x 2
7
8
4
0
7,43
11
11
11
8
13
12
14
3
8
3
8,71
x 1
33
Example - Parameters
?kv Station k Avg.
Model v 1 2 3 4 5 6 7 ?v
1 40 28 44 40 24 40 4 31,43
2
3
t(Sk) 70 63 70 70 35 70 7 55
22
8
22
14
16
0
14,86
22
8
12
13
14
3
8
3
8,71
34
Conclusion
- Station 5 and 7 are not efficiently utilized
- Variation of workload ?kv of stations k is higher
for the models v as for the aggregated model
t(Sk) - Parameters per unit show a high degree of
variation for the models. Model 3, for example,
leads to an high utilization of stations 2, 3,
and 4. - If we want to produce several units of model 3
subsequently, the average cycle time will be
exceeded -gt the line has to be stopped
35
Avoiding unequally utilized stations
- Consider the following objectives
- Out of a set of solutions leading to the same
(minimal) number of stations m (1st objective),
choose the one minimizing the following 2nd
objective - ...Sum of absolute deviation in utilization
- Minimization by, e.g., applying the following
greedy heuristic
36
Thomopoulos heuristic
- Start Deviation ? 0, k 0
- Iteration until not-assigned jobs are available
- increase k by 1
- determine all feasible assignments Sk for the
next station kchoose Sk with the minimum sum of
deviation - ? ? ?(Sk)
37
Thomopoulos example
- T 70
- m 7
- Solution
- 9 stations (min. number of stations 7)
- S1 1, S2 3,6, S3 4,7, S4 8, S5
2, - S6 5,9, S7 10, S8 11, S9 12
- Sum of deviation ? 183,14
38
Thomopoulos heuristic
- Consider only assignments Sk where workload t(Sk)
exceeds a value ? (i.e. avoid high idle times). - Choose a value for ?
- ? small
- well balanced workloads concerning the models
- Maybe too much stations
- ? large
- Stations are not so well balanced
- Rather minimum number of stations very large ? ?
maybe no feasible assignment with t(Sk) ? ?
39
Thomopoulos heuristic Example
- ? 49
- Solution
- 7 stations
- S1 2, S2 1,5, S3 3,4, S4
7,9,10, S5 6,8, S6 11, S7 12 - Sum of deviation ? 134,57
40
Exact solution
- 7 stations
- S1 1,3, S2 2, S3 4,5, S4 6,7,9 ,
S5 8,10, S6 11, S7 12 - Sum of deviation ? 126
?kv Station k Avg.
Modelv 1 2 3 4 5 6 7 ?v
1 40 28 40 36 32 40 4 31,43
2 22 22 16 12 10 22 0 14,86
3 8 13 7 8 14 8 3 8,71
t(Sk) 70 63 63 56 56 70 7 55
41
Further objectives
- Line balancing depends on demand values bj
- Changes in demand ? Balancing has to be reivsed
and further machine set-ups have to be considered - Workaround
- Objectives not depending on demand
- sum of absolute deviations in utilization
per unit
42
Further objectives
- Disadvantages of this objective
- Large deviations for a station (may lead to
interruptions in production). They may be
compensated by lower deviations in other stations - ? ... Maximum deviation in utilization per
unit