Slide sem t

1
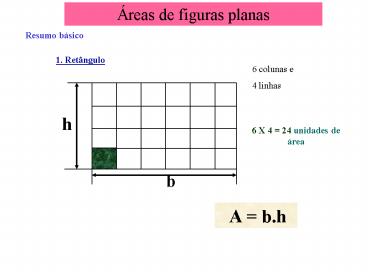
Áreas de figuras planas
Resumo básico
1. Retângulo
6 colunas e 4 linhas
6 X 4 24 unidades de área
A b.h
2
Áreas de figuras planas
Resumo básico
2. Paralelogramo oblíquo
3
Áreas de figuras planas
Resumo básico
2. Paralelogramo oblíquo
A b.h
4
Áreas de figuras planas
Resumo básico
3. Triângulo
h
b
O paralelogramo pode ser dividido em dois
triângulos equivalentes
5
Áreas de figuras planas
Resumo básico
4. Losango
6
Áreas de figuras planas
Resumo básico
5. Trapézio
A área do paralelogramo é ( B b )h
Portanto, cada trapézio tem área
7
Áreas de figuras planas
6. Círculo
Resumo básico
8
Áreas de figuras planas
Cálculos especiais Triângulo equilátero
9
Áreas de figuras planas
Cálculos especiais Fórmula de Herão A área
em função das medidas dos lados
Área
10
Áreas de figuras planas
Cálculos especiais Cálculo da área de um
triângulo em função das medidas de
dois lados adjacentes e o ângulo entre
eles.
11
Áreas de figuras planas
Cálculos especiais Cálculo da área de um
triângulo em função da medida do raio do
círculo inscrito
A p.r
12
Áreas de figuras planas
Cálculos especiais Cálculo da área de um
triângulo em função da medida do raio da
circunferência circunscrita
13
Coroa - Circular
A coroa é formada por um mesmo centro O e raio
R e r. Para obter a sua área é preciso calcular a
diferença da área do círculo maior e do círculo
menor.
A coroa A círculo maior A círculo menor A
coroa (p . R2) - (p . r2) A coroa p . (R2 -
r2)
14
Hexágono Regular
Assim, podemos dizer que a área de um hexágono
regular será igual à soma das seis áreas dos
triângulos eqüiláteros. Logo a área do
Hexágono é
15
(Unicamp-2002) Seis círculos, todos de raio 1cm,
são dispostos no plano conforme mostram as
figuras abaixo a) Calcule a área do triângulo
ABC. b) Calcule a área do paralelogramo MNPQ e
compare-a com a área do triângulo
16
(No Transcript)
17
(No Transcript)
18
a) Área do triângulo
b) Área do paralelogramo
A área do paralelogramo é maior do que a área do
triângulo
19
(Fuvest 2009) A figura a seguir representa sete
hexágonos regulares de lado 1 e um hexágono
maior, cujos vértices coincidem com os centros
de seis dos hexágonos menores. Então, a área do
pentágono hachurado é igual a
a) 3v3 b) 2v3 c) 3(v3)/2 d) v3 e) (v3)/2
20
Resolução
A área S do pentágono hachurado é igual à soma
das áreas de dois triângulos equiláteros
congruentes de lado 1. Assim
e) (v3)/2
Alternativa E