The phase problem - PowerPoint PPT Presentation
1 / 28
Title:
The phase problem
Description:
any material is composed of atoms and it can not be shaped for wavelength of atomic size ... If no related structure is available (ab initio) ... – PowerPoint PPT presentation
Number of Views:88
Avg rating:3.0/5.0
Title: The phase problem
1
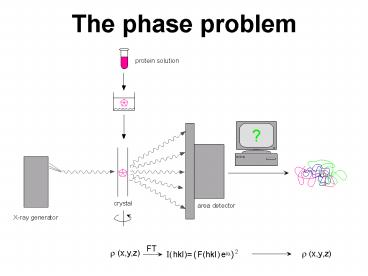
The phase problem
2
The phase problem
- A X-ray microscope is not available
- There are no lenses or mirrors for X-ray
radiation - - any material is composed of atoms and it can
not be shaped for wavelength of atomic size - the refractive index of all material is very
close to vacuum - radiation damage
3
The phase problem
F(hkl)
imag axis
2pi (hxkylz) F(hkl) ?
fj e j
?
real axis
1
r
i
a
(
hk
l
)
-
2
p
i
(
hx
ky
lz
)
(
x y z
)
? ? ?
F
(
hkl
)
e
e
v
h
k
l
The phase is more important than the structure
factor.
4
Phase determination
- If no related structure is available (ab initio)
- method of multiple isomorphous replacement (MIR)
- method of multiple anomalous dispersion (MAD)
- direct methods
- if a related structure is available
- method of molecular replacement (MR)
5
MIR method
- Based on binding of a heavy atom to the protein
crystal - intensity of each reflection is changed
- The phases are derived from the difference of the
structure factor - amplitude of the protein crystal with and without
heavy atom - FPH- FP
6
Steps of the MIR method
- Preparation of heavy atom derivatives (protein
crystals - are soaked with a heavy atom solution)
- Data collection of a crystal soaked with a heavy
atom - Determination of the heavy atom position in the
- unit cell
- Refinement of the heavy atom position
- Determination of the phase angle of each
reflection
7
Determination of the position of the heavy atom
within the unit cell
1. Difference Patterson method 2. direct method
8
Difference Patterson method
V Patterson function
P(uvw) V ? ?(xi,yi,zi) ?(xiu, yiv, ziw)
i
y
The Patterson function at a certain point uvw is
given from the product of the electron density
at the point x,y,z with the electron density at
the point x,y,z u,v,w. It will be summed up
about all volume elements i. V is number of
volume elements.
x
P(u,v,w) will have a high value at the point uvw,
if ?(xi,yi,zi) und ?(xiu, yiv, ziw) are also
high. The Patterson function shows us also the
distance between regions of high
electron density (atoms) in the EZ.
v
u
9
Difference Patterson method
V
Patterson-Funktion P(uvw) V ? ?i(x,y,z)
?i(xu, yv, zw)
i Da ?i(x,y,z) 1/V ? Fhkl exp
-2?i(hx ky lz)
V P(u,v,w) 1/V2 ? ? FhklFhkl
exp-2?i(hu kv lw ? exp 2?i((hh)xi
(kk)yi (ll)zi)
h h
i
0 except h -h, k -k, l -l
P(u,v,w) 1/V ? F2h exp2?i(hu kv lw 1/V ?
F2-h exp-2?i(hu kv lw
As cosa 1/2 (exp(i?) exp (-i?)) P(uvw) 2/V
???F(hkl)2 cos 2?(hu kv lw) The Patterson
function is a real function, which only contains
measured intensities.
10
Difference-Patterson method
P(uvw) 2/V ???(FPH -FP)2 cos 2?(hu kv lw)
?Fiso
?Fiso FPH - FP ?Fiso FH cos(?PH - ?H)
FH
FP
(?PH - ?H)
FPH
(?Fiso)2 FH2 cos2(?PH - ?H) (?Fiso)2
½FH2 ½FH2 cos 2(?PH - ?H) In the
Difference-Patterson map includes the 2. term
only noise, as ?PH and ?H are not correlated.
Therefore, the distances between the heavy atoms
are obtained.
11
Difference-Patterson method
P(uvw) 2/V ???(FPH-FP)2 cos 2?(hu kv lw)
u1 x1 x1 2x1 w1 z1 z1 2z1 v1 0
z.B. P2 x,y,z -x,y,-z
x
u
v 0 Harker- plane
2
u1
u1
1
3
w
z
3
1
-u1
-u1
2
12
Determination of the structure factor of the
heavy atom
sin2? FH(hkl) ? An fn exp- Bn ??? exp 2pi
(hxn kyn lzn) FH exp i?p
n ? fn atom
scattering factor An occupancy Bn temperature
factor xn, yn, zn x,y,z-coordinates of the heavy
atom n
13
Determination of the phase angle
imag. axis
Harker construction (by one heavy atom derivative)
FP
FPH1 FP FH1
FPH1
0
real axis
-FH1
intersection point of the circle corresponds to
2 possible phase angles
14
Determination of the phase angle
imag. axis
Harker construction (by 2 heavy atom derivatives)
FP
FPH2
FPH1 FP FH1 FPH2 FP FH2
FPH1
0
real axis
-FH1
-FH2
15
Determination of the phase angle
Due to several errors (measurement error,
nonisomorphy) an exact intersection point of the
3 circles will never be observed. How we can
obtain the optimal phase?
? lack of closure error (error attributed
to derivative data) ? FPH(obs) - FPH(calc)
small ? small phase error
16
P(?)
Assume a Gaussian error distribution, the phase
probability P(?) for a reflection related to a
derivative is ?2
(?) N normalis. fact. P(?) N exp - ??? E
average of ? 2E2
Fp
For several derivates
n ?j2
(?) P(?) ? Pj(?) N exp -? ???
j1 2Ej2
Fp
17
How you can get the best phase?
? P(?) Fp(?) Fbest ?????
? P(?)
P(?)
C
The best value for Fp is the weighted average of
all Fp. Fbest points to the centre of the
probability distribution of Fp.
?best
Fbest
Fp
With Fbest Fbest exp i?best and Fp Fp exp
i?
Fp ? P(?) cos ? Fbest
cos ?best ???????
? P(?)
Fp ? P(?) sin ? Fbest sin ?best ???????
?
P(?)
C
?best
Fbest
Fp
2 equations, 2 unknowns
18
Refinement of the heavy atom positions
sin2? FH(hkl) ? An fn exp- Bn ??? exp 2pi
(hxn kyn lzn) FH exp i?p
n ? fn atomic
scattering factor An occupancy Bn temperature
factor xn, yn, zn x,y,z-coordinates to the heavy
atom n
FPH(calc)
FPH(calc) Fp2 FH2 2Fp FH cos(??H -
?P)1/2
sin2? M ? ? k FPH(obs) exp- B ??? -
(FPHcalc)j2 hkl
? ? weighting factor (often m) k scale
factor B temperature factor
19
Quality of the phase angle
1. figure of merit
F(best) ?m m
???? for each reflection m ???
gt 0.5 F
N
2. Rcullis Faktor
?(FPH - FP) -
FH Rj (Cullis) ?????????? pro
Derivat lt 0.7 ?
FPH - FP
3. Phasing power
?FH(calc)
phasing power ????? pro
Derivat gt 1.0
? E ? E FPH(obs) - FPH(calc)
20
MAD method
- based on the fact that electrons are not free
but - bound to an atom nucleus.
- (anomalous scattering)
- Scattering of an electronic dipol oscillator
- ?2
f scattering
factor - f ?????? ? frequency of the
incident beam - ?2 - ?s2 -ik? ?s resonance
frequence i.e. - absorption frequency
- k damping factor
- Ist ? gtgt ?s f ?1 Scattering of one
electron - Ist ?s gtgt ? f ?0 no scattering as electron
is fixed - Ist ? ? ?s only now an imaginary part is
relevant
21
MAD method
Other formulation fanom f ?f if f
if
imag
fanom
f
real
f
? f
Friedel law breaks FP(hkl) ? FP(-h-k-l)
22
MAD method
protein anomalous scatterer
anomalous scatterer
FP(hkl)
imag
f
fanom
?f
FH
FP(-h-k-l)
f
real
f atom scattering factor of the anomalous
scatterer away from an absorption edge ?f real
contribution of the absorption edge f
imaginary contribution of the absorption edge
FP(hkl) ? FP(-h-k-l)
23
Steps of the MAD method
1. Expression of proteins, in a medium that
contains only Se-methionine an intrinsic
anomalous scatterer binding of an anomalous
scatterer 2. crystallisation 3. Data collection
by different wavelengths 4. Determination of the
positions of the scatterers in the unit cell 5.
Refinement of the positions of the scatterers 6.
Determination of the phase angle of each
reflection
24
Data collection of a crystal by different
wavelengths
3 wavelengths 1. ?1 ? ?f1 is minimal ?
f1 is the turning point 2. ?2 ? f2 is
maximal, (Fp2(h) - Fp2(-h)) is maximal 3.
?3 ? ?f3, f3 is small,(far away
from the absorption edge) (Fp3(h) - Fp1(h)) is
maximal
Wavelengths ?1und ?2 have to determined exactly
to optimize the difference between FP(h) and
FP(-h).
25
Determination of the position of the scatter
P(uvw) 2/V ??? ?F2 cos 2?(hu kv lw)
?F ?(Fp2(h) - Fp2(-h)) FH ?F
?(Fp3(h) - Fp1(h)) FH
Phase determination
circle F?3
circle F?1
analogous to the MIR method one data set at one
wavelengths is chosen as reference data set.
FH
26
Phase determination
For several wavelengths
n ?j2
(?) P(?) ? Pj(?) N exp -? ???
j1 2Ej2
? Fbest, ?best
??3-?1
FHA
??2
F?1
F?2(-h)
FHA
F?3
F?2(h)
FA
FB
FB F of the atoms that do not scatter anomalous
FA not anomalous contribution to F of the
anom. scattering atoms
27
Combination of MIR and MAD
28
Berechnung der Elektronendichtekarte
1 i ?best(hkl)
-2pi (hx ky lz) ?(x y z) ? ? ? ? m(hkl)
Fbest(hkl) e e
V h k l