Diapositive 1

1
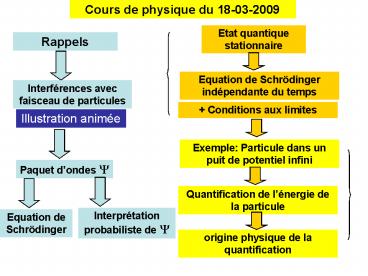
Cours de physique du 18-03-2009
Etat quantique stationnaire
Rappels
Equation de Schrödinger indépendante du temps
Interférences avec faisceau de particules
Conditions aux limites
Illustration animée
Exemple Particule dans un puit de potentiel
infini
Paquet dondes ?
Quantification de lénergie de la particule
Interprétation probabiliste de ?
Equation de Schrödinger
origine physique de la quantification
2
Interférences ? particule ? paquet donde
paquet donde ? probabilité de présence de la
particule ponctuelle.
3
Interférences avec des particules (animation)
4
particule libre paquet donde gaussien
Probabilité de présence de la particule
5
Incertitude du résultat dune mesure
Position et vitesse incertaines
Trajectoire
Mécanique quantique
Mécanique classique
6
Etat (dynamique) stationnaire
Mouvement
Energie variable
E(t)
Propriétés indépendantes du temps
Non-stationnaire
permanence
Energie constante
(Périodicité)
7
Etat dynamique stationnaire quantique
position et vitesse incertaines
Mouvement
Probabilité indépendante du temps
Energie constante
8
Probabilités
9
Rappel Equation de Schrödinger
Particule libre
Particule dans un potentiel
10
Etats stationnaires
Equation de Schrödinger indépendante du temps
11
Détermination des états stationnaires
Fonction de carré sommable
Norme1
12
Entracte 15 minutes
13
Détermination des états stationnaires
14
Particule de masse m dans un puit de potentiel
infini
15
Mécanique classique
Etat classique de la particule
2
16
Mécanique quantique
17
Solution
1) Equation de Schrödinger des états
stationnaires Egt0
18
Solution
Quantification de lénergie
2) Conditions aux limites
0
a
19
Solution
3) Norme (Carré sommable)
a
0
n?1, ?2, ?3,... Etats possibles de la particule
n Nombre quantique
20
Etats quantiques possibles de la particule
?2
E
21
origine mathématique de la quantification
discrète des énergies possibles
?2
E
22
origine physique de la quantification discrète
des énergies possibles
?2
E
Onde stationnaire noeuds en 0 et en a
Interférence non-destructive segment fini
23
origine physique de la quantification discrète
des énergies possibles
?2
Interférence destructive
24
origine physique de la quantification discrète
des énergies possibles
?2
Interférence destructive
(k,E) ?
Pas de confinement spatial
25
Quantification discrète des énergies
1) Particules ondes
2) Auto-interférences non destructives
3) Confinement spatial
(Cavité en résonance)
Electron noyau
Etats liésatome
E quelconque
E valeurs discrètes
Diffusion, ionisation
26
The End (for today)