Chapter 6: Boltzmann Statistics

1
Chapter 6 Boltzmann Statistics
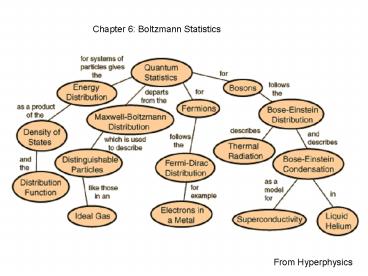
From Hyperphysics
2
Maxwell Boltzmann statistics applies to
distinguishable particles

• Distinguishable classical (no quantum effects)
• Any of particles can occupy a given state
• At thermal eq, the particles will take the most
  probable distribution, based on Etotal and Ntotal
• Every specific microstate si of the system has
  equal probability
• These assumptions lead to the proper (Boltzmann)
  distribution of particles in the energy states
• but yield non-physical results for the entropy
  (Gibbs paradox)

3
9 units of energy distributed among 6
distinguishable particles
Probability of finding a system in (micro)state s
depends on how many total microstates there are.
4
Canonical ensemble
System of interest is immersed in heat reservoir.
The two systems are in thermal contact (exchange
energy only). It is drawn this way to show that
the total system is different from the reservoir.
5
Prob. that the atom will be in state s
When E is large, it is less likely that the atom
will be in that state
At higher T, it is more likely that the atom will
have energy E
6
(No Transcript)
7
(No Transcript)
8
Application of Boltzmann statistics to Diatomic
molecules
Each energy has a degeneracy of 2j1
9
Probability density function
10
Rotational spectrum of HCl
11
(No Transcript)
12
Maxwell speed distribution (per mole, not per
molecule so D(v) is called f(v) here)
13
(No Transcript)
14
Distribution of particle speeds for 106 oxygen
molecules at -100, 20 and 600oC
15
Problem 6-39