Orbits

1
(No Transcript)
2

• Orbits Gravity

3
Tycho Brahe (1546 1601) Tee-ko Bra
A Danish nobleman and astronomer His most
significant contribution to science Nearly 30
years of his life was spent accurately
documenting the position of the planets against
the backdrop of the Celestial Sphere.
4
Tychos luxurious pretelescope-era observatory
on the island of Hven where most of his data was
collected.
5
After nearly 30 years of observations, Tycho
could not find a satisfactory model that
supported the Copernican universe. He eventually
settled for a more Aristotelian model.
6
Disagreements with the sovereign forced Tycho to
leave his plush accommodations in Denmark for
Prague in the summer of 1599 While in Prague,
Tycho hired a young German mathematician to
assist Tycho in is quest to develop a working
model of the universe. This troubled young
genius would provide a strikingly simply and
beautiful model of the planetary motions
Rudolph II (sitting) contemplates Tychos Universe
Eduard Ender (1855)
www.mhs.ox.ac.uk/tycho/
7
Johanes Kepler (1571 1630)
A Copernican Introversive, referred to himself
as the mangy dog Brilliantly disciplined in
the use of mathematics Developed three laws of
planetary motion based on Brahes extensive data
collection
8
If I had believed that we could ignore these
eight minutes of arc, I would have patched up
my hypothesis accordingly. But, since it was not
permissible to ignore, those eight minutes
pointed the road to a complete reformation in
astronomy Johannes Kepler
9
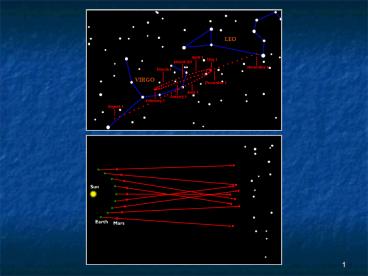
(No Transcript)
10
Keplers Laws are based on the mathematics/geometr
y associated with conic sections
11
Note that every ellipse has two focal points
12
Eccentricity, e, is a quantitative measure of the
degree to which an object deviates from being
circular.
Note that for a circle the eccentricity is zero
and for an increasingly elliptical shape, the
eccentricity is approaching 1. A parabolic
path has an e equal to 1 and a hyperbolic path
has an e greater than 1 but less than infinity.
13
Keplers 1st LawLaw of Orbits
14
Note that none of the planets within our solar
system have orbits that are perfect circles.
(the eccentricity is not zero)
15
Planets are not the only objects that follow
conic paths around the Sun And the Sun is not
the only object that has objects orbiting it.
Keplers Laws apply equally well to the moon
around the Earth and any other object orbiting
another!
16
(No Transcript)
17
Keplers 2nd LawLaw of Areas
Note that equal areas are covered by a line
extending from the Sun to the orbiting object in
equal time intervals
18
Keplers 3rd LawLaw of Periods (Harmony of
Spheres)
Note that square of the orbital period (p) of
each planet is equal to the cube of the semimajor
axis (a).
19
Isaac Newton

• 1642-1727
• Achievements
• Calculus
• Laws of Motion
• Law of Gravitation
• Nature of Light
• Adv. Telescopes
• Just to name a few!!

20
1st Law of Motion

• Every body continues in its state of rest, or of
  uniform motion in a right straight line, unless
  it is compelled to change that state by a force
  impressed on it.
• This law is often referred to as The Law of
  Inertia and is credited as an accomplishment of
  Galileo.

21
1st Law of Motion

• This is what Newton would refer to as natural
  motion or inertial motion.
• Note that Force is not required for objects to
  be in or maintain motion.

22
2nd Law of Motion

• The change in motion is proportional to the
  motive force impressed and is made in the
  direction of the right line in which that force
  is impressed.

23
2nd Law of Motion

• The change in motion (acceleration) is
  proportional to the motive force impressed and
  is made in the direction of the right line in
  which that force is impressed.

24
2nd Law of Motion

• The unit of force is given the name Newton N.
• Based on Fma, the unit of a newton can be
  expressed as
• 1 Newton (1kilogram)(1meter)
• (second)2

25
3rd Law of Motion

• To Every action there is always an equal
  reaction or, the mutual actions of two bodies
  are always equal, and directed to contrary parts
  opposite directions.

26
3rd Law of Motion

• If motion was bestowed upon one object it must
  have been taken from another.

What if this astronauts jetpack fails? How can
he get back to the ship? Knowledge of Newtons
3rd will save his life!!
27
3rd Law of Motion

• FBC FCB
• As the book leans and pushes on the crate, the
  crate pushes with an equal and oppositely
  directed force on the book.

28
3rd Law of Motion

• FEarth on Ball FBall on Earth
• Each time the ball bounces off the Earth, the
  Earth and ball exert forces on each other.
  According to Newtons 3rd law, these forces are
  exactly the same in magnitude and in opposite
  directions. Why is it that the ball is the only
  object visible changing direction?

29
Newtons Universal Law of Gravitation
Projectile motion on Earth had been well
documented before Newton but the models of motion
lacked a mechanism for the movement towards
Earth. Newton envisioned a force that gives
every object with mass the ability to reach
across empty space and pull on neighboring
bodies of mass. GRAVITY
30
Newtons Universal Law of Gravitation

• The force that one massive body exerts on another
  such that the two bodies are drawn together is
  directly proportional to the masses of each body
  and inversely proportional to the separation
  distance of the two bodies.
• Written in the form of Newtons 2nd Law
• F ma Fg G(m1m2)/r2 m1(Gm2/r2)
• where G is a constant of proportionality given by
  the value 6.67x10-11 Nm2/kg2
• The value of G was never known to Newton! It
  would not be discovered until about 1800 by Henry
  Cavendish.

31
Newtons Universal Law of Gravitation

• The value of G was never known to Newton! It
  would not be adequately measured experimentally
  until 1798 by Henry Cavendish.

Cavendishs Torsion Balance Used to estimate the
universal gravitational constant, G
Henry Cavendish (1731-1810)
32
Newtons Universal Law of Gravitation

• How could Newton extend his idea of Earthly
  gravitation to the motion of the celestial
  bodies?
• The moon was the key!

33
Newtons Universal Law of Gravitation

• If an apple falls towards the Earth due to
  gravity, does this same gravitational force
  extend into the heavens? Is it the same force
  that keeps the Moon in orbit around the Earth?

34
Consideration of Uniform Circular Motion

• The acceleration of any object undergoing uniform
  circular motion is
• This is based on simple motion experiments
  performed here on Earth. The acceleration in
  this type of motion is known as Centripetal
  Acceleration (or center-seeking acceleration)

35
Acceleration of the Moon Towardsthe
Earth(Approximating it to be Uniform Circular
motion)

• The Moon moves around the Earth in a nearly
  uniform circular orbit with a speed of 1016m/s.
• The distance between the Moon and Earth is known
  to be 3.8x108m.
• Approximating the motion to be uniform and
  circular yields a centripetal acceleration of
• amoon v2/r (1016m/s)2/(380 000 000m)
• amoon 0.00272m/s2

36
Acceleration of the Moon Towards the Earth(Using
Newtons Gravitational Inverse Square Law)

• Newton then imagined his gravitational force
  extending out into the heavens and pulling on the
  Moon.
• Since the distance to the Moon is about 60 times
  longer than the radius of the Earth, Earths
  gravity should be considerably weaker at the
  Moons location.
• Based on earthly experimentation, things
  accelerate downwards at a rate of 9.81m/s2 when
  near the surface of the Earth.
• Assuming an inverse square law relationship
  between gravity and distance, Newton supposed
  that the Earths gravitational acceleration
  should be about 602 times less (3600 times less)
  near the Moon than it is on Earth.
• amoon (9.81m/s2)/3600
• amoon 0.00271m/s2

37
Gravity

• Newton found the connection
• The forces (gravity) that govern projectile
  motion here on planet Earth ALSO govern the
  motion of the moon the planets.
• REVOLUTIONARY THINKING!!!

38
Newtons Gravitation and Keplers Laws

• Keplers 3rd law (p2 a3) can be derived (with a
  little algebra calculus) from Newtons Law of
  Gravitation.
• (M1 M2)p2 8a3
• Where a is the semimajor axis length, P is the
  period of orbit, and the Ms are the masses of
  the orbiting objects

39
Newtons Gravitation and Keplers Laws

• (M1 M2)p2 8 a3
• Newton had given a mechanism for Keplers
  planetary motion laws
• With this relationship, we can measure distances
  and periods by observation and then calculate the
  mass of any object orbiting another!!

40
The masses of the stars and planets

• G(M1 M2)p2 4pa3
• It is from this relationship that we estimate the
  mass of the Sun, the planets, and any other
  celestial body orbiting another!!
• Keypoint Masses of Celestial objects are
  derived from observing orbital motion of the
  objects.
• (No one has yet invented a universal scale to
  place under the planets and stars.)

41
History recalls that nearly 20 years passed
before Newton was urged by his contemporary, Sir
Edmund Halley, to publish his results (and claim
Christopher Wrens prize for explaining Keplers
Laws of planetary motion). Newtons laws
of motion and gravity were first published in
1687 as Philosophiae Naturalis Principia
Mathematica.
Edmund Halley (1656-1742)
Christopher Wren (1632-1723)
42
Earth/Moon Gravitational Effects
Phases of the Moon What causes them?
The Earth and Moon exert mutual gravitational
forces on each other Every particle on the
Earth is influenced by the gravitational force of
the Moon This has a small effect on the hard
surface of the Earth However, the effect is
quite noticeable on the Earths liquid surface
(oceans)
Fig 3-13, p.72
43
Ocean Tides
Phases of the Moon What causes them?
Two tidal bulges are caused by the pull of the
moon There is a tidal bulge on the moon side of
the Earth due to strong lunar gravity and
another directly on the other side due to weak
lunar gravity and the fact that the Earth is
accelerating towards the moon (essentially
leaving the water behind)
44
Ocean Tides
45
The Sun Ocean Tides
Phases of the Moon What causes them?
The Sun can also influence the tides (but to a
lesser degree) When the Sun and Moon lie on the a
line that passes through Earth (either on
different sides, Full Moon or on the same side,
New Moon) the tides are higher and are called
Spring Tides (nothing to do with Spring
season) When the Sun and Moon lie on
perpendicular lines relative to Earth (either
first quarter or third quarter) the tides are
lower and are called Neap tides.