Untitled

1
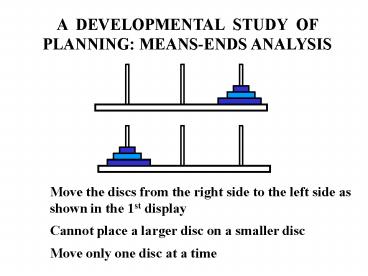
A DEVELOPMENTAL STUDY OF PLANNING MEANS-ENDS
ANALYSIS
Move the discs from the right side to the left
side as shown in the 1st display Cannot place a
larger disc on a smaller disc Move only one disc
at a time
2
DEVELOPMENTAL FINDINGS FROM THE TOWER OF HANOI
PROBLEM
Performance success from 3 to 6 yrs older
children can solve problems with more moves
What happens when a child cant move a disc
directly toward the goal younger children
break the rules older children start to plan
moves in advance
3
Case Study Helping Children Solve The Tower of
Hanoi Problem Aiding Representation and
Lessening the Cognitive Load
Provide the child a Meaningful Story so the task
becomes more comprehensible
Represent Goal State so the child doesnt have to
keep it in mind.
Incorporate the Key Rule about placing larger
discs on smaller ones in the actual task materials
4
IMPORTANT PROBLM-SOLVING PROCESSES CAUSAL
INFERENCE
Contiguity events occur close together in
time and space
Precedence event labeled cause precedes
event labeled effect
Covariation cause and effect consistently
occur together
5
DEVELOPMENTAL FINDINGS CAUSAL INFERENCE
Contiguity infants in their 1st year already
use both temporal spatial contiguity to
infer causality
Precedence By age 5 children consistently use
the order of events (A-B-C) to infer
cause-effect
Covariation By age 8 children can use
consistent co- occurrence to infer causality
even with a time delay
6
The Role of Analogy in Problem Solving (Gick
Holyoak, 1983) Problem 1 How to irradiate a
tumor without harming surrounding
tissue. Solution Attack tumor from many
different angles with weak x-rays
At the point of intersect (tumor) x-rays are
full strength. Problem 2 How to attack a
fortress without losing men on the roads into the
fortress which are mined and prevent a large army
from approaching the fortress. Solution Break
up army and approach fortress in small groups
from many of the roads when the small forces
meet at the fortress, the army will be at full
strength.
7
Results Gick Holyoak (1983) Percentage of
subjects who see the relation across
problems One story analog before the radiation
problem 29 Two story analogs before the
radiation problem 45 Two story analogs plus
a principle 62 Principle The general
attributed his success to an important principle
If you need a large force to accomplish some
purpose, but are pre-vented from applying such a
force directly, many smaller forces applied
simultaneously from different directions may work
just as well.
8
A Child Study Of Analogical Reasoning 3, 4 and 5
year old children are presented with a three
dimensional display and given a simple problem.
They are asked to enact the solution. Problem
1 John, the garage mechanic, has a problem. He
needs to take all of the tires that have been
delivered to his garage and put them up on a
shelf. But the shelf is too high and he doesnt
have a ladder so he cant reach the shelf
by himself. How can he solve his
problem? Solution Stack two tires and stand on
top of them. Problem 2 Bill, the farmer, has a
problem. He needs to put his bales of hay on top
of his tractor so he can take them to the market.
But Bill isnt tall enough to reach the top of
the tractor by himself. How can he solve his
problem? Solution Stack two tires and stand on
top of them.
9
Helping Children Engage in Analogical
Reasoning Seeing past superficial differences
Verbally prompt child to describe
problem solutions across different problems
Use three dimensional displays and have the
children enact the solutions
Use multiple examples of problems with the same
solution
10
IMPORTANT PROBLM-SOLVING PROCESSES SCIENTIFIC
LOGICAL REASONING

• Do children understand the logic of
• experimentation?

Not until they approach formal operations

• Do children understand the logic of
• deductive reasoning?

Not fully until they approach formal operations
and receive explicit instruction
11
Jean Piaget Mixing Colors Problem
Classic Problem

• 1,2,3,and 4 contain colorless, odorless liquids.
• X contains an activating solution.
• Some combination of liquids (always including X)
• will give a YELLOW color.
• How can you find the combination that
• makes YELLOW?

X
Jean Piaget (1896-1980) Childrens Cognitive
Development University of Geneva
1
2
3
4
12
Jean Piaget Mixing Colors Problem
Classic Problem
1x 2x 3x 4x
12x 13x 14x 23x 24x 34x
123x 124x 134x 234x
1234x
Jean Piaget (1896-1980) Childrens Cognitive
Development University of Geneva
13
Classic Problem
Jean Piaget Rods Task
Steel
Copper
Brass
14
CONTROL OF VARIABLES CANAL PROBLEM
You are asked to determine how canals should be
designed to optimize boat speed. Working with an
actual canal system and timing the boats from
start to finish, you can conduct experiments to
identify factors that influence speed. (boats are
towed with a string and pulley system)
Variables large and small boats square,
circular, and diamond shaped boats canal can be
shallow or deep you can make a boat heavier by
adding a barrel Counterintuitive boats are
faster in deeper canal, shallow canal due to
greater turbulence
15
CONTROL OF VARIABLES CANAL PROBLEM
A typical 11 year old childs experimentation
Trial 1 small, circular, light boat in a
deep canal Trial 2 large, square, heavy
boat in a shallow canal After Trial 2, the child
concluded that weight makes a difference, but
when asked to justify the conclusion, he simple
said that if the boat in Trial 2 had been light
it would have gone faster. Trial 3 small,
diamond-shaped, light boat in a shallow
canal Child predicts that the boat in Trial 3
would go faster than the boat in Trial 2 because
it depends on how much edging is on the thing
(a hypothesis about the shape) Note child
fails to systematically test hypotheses, only
notices confirmatory evidence
16
CONTROL OF VARIABLES CANAL PROBLEM
A college students experimentation After
numerous trials the student summarizes what she
has accomplished so far. Well, so far we worked
with small boats. First, light, and then we
added the weight to each of them, and we found
that without the weight they would go faster. We
also found out that the diamond shape was the
fastest, with the circle being next. And the
slowest was the square. Lets take the bigger
boats in the deeper water. Well start with the
square and go in order. Student notices the
counterintuitive result with depth of canal. She
immediately searches for a plausible
explanation. My God! It does have an effect! It
takes longer in shallow water! The only thing I
can figure out is that the depth of water would
have something to do with the buoyancy. The
added water, adds more buoyancy, making the boat
sit up higher in the water.
17
UNDERSTANDING THE DIFFERENCE BETWEEN DEDUCTIVE
INDUCTIVE REASONING
Deductive Problem All poggops wear blue boots
Tombor is a poggop Does Tombor wear blue
boots?
Inductive Problem Tombor is a poggop
Tombor wears blue boots Do all poggops wear
blue boots?
Developmental Findings Kindergarteners see
both conclusions as true 4th graders judge
the deductive problem as true
18
UNDERSTANDING THE DIFFERENCE BETWEEN DEDUCTIVE
REASONING GUESSING
Two toys are hidden in two different boxes
Puppet looks in one container and sees a red
toy, so concludes the blue toy is in the other
box How certain is the puppet?
Two toys are hidden in two different boxes
Puppet announces that the red toy is in box 1
How certain is the puppet?
Developmental Findings 4 yr olds dont see any
difference in the problems, by 9 yrs all children
knew the 1st problem was certain