Efficiently Selecting Regions for Scene Understanding - PowerPoint PPT Presentation
Title:
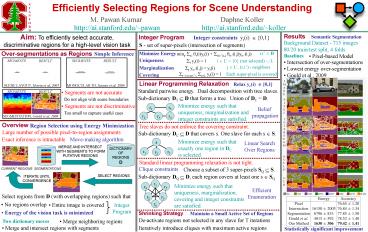
Efficiently Selecting Regions for Scene Understanding
Description:
Title: PowerPoint Presentation Author: bnk bnk Last modified by: phil gooby Created Date: 6/6/2006 2:03:31 PM Document presentation format: Custom Company – PowerPoint PPT presentation
Number of Views:16
Avg rating:3.0/5.0
Title: Efficiently Selecting Regions for Scene Understanding
1
Efficiently Selecting Regions for Scene
Understanding
S T A N F O R D
M. Pawan Kumar Daphne Koller
http//ai.stanford.edu/pawan http//ai.stanford.edu/koller
Aim To efficiently select accurate,
discriminative regions for a high-level vision
task
Results
Integer Program
Semantic Segmentation
Integer constraints yr(i) ? 0,1
Background Dataset - 715 images
S - set of super-pixels (intersection of segments)
80/20 train/test split, 4 folds
Over-segmentations as Regions
Minimize Energy
r,r ? D
Simple Inference
miny ?r,i ?r(i)yr(i) ?(r,r),i,j
?rr(i,j)yrr(i,j)
Baselines
- Pixel-based Model
Uniqueness
?i yr(i) 1
i ? L 0 (not selected) ? L
SEGMENTS
SEGMENTS
RESULT
RESULT
- Intersection of over-segmentations
j ? L, (r,r) - neighbors
Marginalization
?j yrr(i,j) yr(i)
- Lowest energy over-segmentation
?r covers s ?i?L yr(i) 1
Each super-pixel is covered
Covering
- Gould et al., 2009
I M A G E
Linear Programming Relaxation
Relax yr(i) ? 0,1
SCENE LAYOUT, Hoiem et al, 2005
MONOCULAR 3D, Saxena et al, 2008
Standard pairwise energy. Dual decomposition
with tree slaves.
- Segments are not accurate
- Do not align with scene boundaries
SEGMENTS
RESULT
Sub-dictionary DT ? D that forms a tree. Union
of DT D.
P I X E L
Minimize energy such that uniqueness,
marginalization and integer constraints are
satisfied.
- Segments are not discriminative
- Too small to capture useful cues
r1
r5
Belief propagation
r2
r3
r4
SEGMENTATION, Gould et al, 2008
I N T E R
Overview
Region Selection using Energy Minimization
Tree slaves do not enforce the covering
constraint.
Large number of possible pixel-to-region
assignments
Sub-dictionary DC ? D that covers s. One slave
for each s ? S.
S E G M
Exact inference is intractable
Move-making algorithm
s
Minimize energy such that exactly one region in
DC is selected.
Linear Search Over Regions
DICTIONARY OF REGIONS D
MERGE AND INTERSECT WITH SEGMENTS TO
FORM PUTATIVE REGIONS
r1
r3
r2
G O U L D
Standard linear programming relaxation is not
tight.
Clique constraints
Choose a subset of 3 super-pixels SQ ? S.
SEGMENTATIONS
CURRENT REGIONS
Sub-dictionary DQ ? D, each region covers at
least one s ? SQ
SELECT REGIONS
ITERATE UNTIL CONVERGENCE
O U R
Minimize energy such that uniqueness,
marginalization, covering and integer constraints
are satisfied.
Efficient Enumeration
Select regions from D (with overlapping regions)
such that
- No regions overlap
- Entire image is covered
Integer Program
- Energy of the vision task is minimized
Shrinking Strategy
Maintain a Small Active Set of Regions
De-activate regions not selected in any slave for
T iterations
Two dictionary moves
- Merge neighboring regions
- Merge and intersect regions with segments
Iteratively introduce cliques with maximum active
regions
Statistically significant improvement