Cumulus - PowerPoint PPT Presentation
1 / 28
Title:
Cumulus
Description:
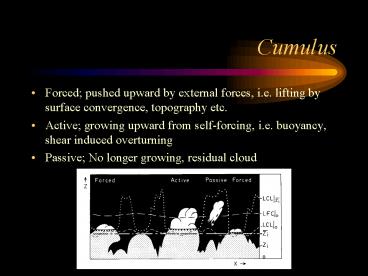
Cumulus Forced; pushed upward by external forces, i.e. lifting by surface convergence, topography etc. Active; growing upward from self-forcing, i.e. buoyancy, shear ... – PowerPoint PPT presentation
Number of Views:106
Avg rating:3.0/5.0
Title: Cumulus
1
Cumulus
- Forced pushed upward by external forces, i.e.
lifting by surface convergence, topography etc. - Active growing upward from self-forcing, i.e.
buoyancy, shear induced overturning - Passive No longer growing, residual cloud
2
Cumulus Clouds
- Shallow Cumulus (cumulus, scatted cumulus,
strato-cumulus) - Depth small compared to scale height of
troposphere, i.e. - Usually confined to Planetary Boundary Layer
(PBL) - Typically non-precipitating
- Surface friction plays critical role to
organization - Deep Cumulus (congestus, cumulonimbi)
- Depth comparable to scale height of troposphere
- Precipitating
- Friction plays secondary role to organization
3
Instabilities Resulting in Cumulus
- Three basic atmospheric flow instabilities
- Inertial Instability Against horizontal inertial
balance, i.e. horizontal pressure gradient,
coriolis and centrifugal force - Static Instability (absolute instability)
Against vertical hydrostatic balance, i.e.
vertical pressure gradient and gravity force - Symmetric Instability Against inertial balance
on an isentropic (constant potential temperature)
surface, i.e. isentropic pressure gradient force,
coriolis and isentropic centrifugal force (a
combination of 1 and 2! Think about this!)
4
Symmetric Instability
5
Instabilities Resulting in Cumulus
- Conditional, i.e. only if saturated
- (CI) Conditional (static) instability
- (CSI) Conditional Symmetric Instability
- Frictional, i.e. in the PBL
- Rayleigh- Bernard
- Inflection Point Instability
- (KH) Kelvin-Helmholtz
- Gravity Wave Resonance
6
Kelvin-Helmholtz Instability
- Small perturbation tends to amplify by the
advection of vorticity (shear gt curvature) - Resistance to growth of wave by static stability,
i.e. Brunt-Vaisalla Frequency, N - Condition for instability
7
(No Transcript)
8
(No Transcript)
9
Rayleigh-Benard Instability
- Results when a thin layer of fluid is subjected
to heat fluxes from top or bottom of layer - Forces
- Promoting overturning heat flux
- Resisting overturning friction
10
Rayleigh Number
- Non-dimensional number depicting ratio of heat
flux or buoyancy forcing to frictional
resistance - h is fluid depth (m)
- ? is the lapse rate (K/m)
- ae is the coefficient of expansion
- D is the viscosity (m2/s)
- K is the thermal conductivity (K m/s)
11
Condition forRayleigh-Benard Instability
- Linearize Navier stokes equations
- Assume wave solution
- Then the condition for instability is
12
Condition for Rayleigh-Benard Instability
- Instability for any number of combinations of k
and l including - Cells
- Rolls
- The value that Ra must exceed is a function of
horizontal wave number
13
Most Unstable Rayleigh-Benard Mode
- Differentiate stability condition w.r.t.
horizontal wave number and set to zero to obtain
condition for maximum (growth rate) - If for simplicity we assume and
we assume square cells
where S is the spacing, then a ratio of
horizontal spacing to depth Sh31 is implied.
14
Hexagonal form to Rayleigh Benard Convection
15
Organization of Boundary Layer Convection
- Cellular (Rayleigh-Benard)
- Closed Cells
- Open Cells
- Linear
- Wind Parallel (Rayleigh-Benard)
- Inflection Point (Kelvin-Helmholtz)
- Gravity Wave Resonance
- Spoked (Rayleigh-Benard)
- Actinae
16
Cellular Convection
17
Mesoscale Cellular Convection (MCC)
18
Linear Convection
19
Open, Closed and Actinae Convection
20
Linear,Roll-type Convection
21
Hexagonal Cells
22
Cellular Convection
- Also known as mesoscale Cellular Convection (MCC)
- Two types
- Type I typically to the east of continents
during the winter season over warm ocean currents
(driven by heating from below) - Type II Occur during the summer to the west of
continents over cool ocean currents (driven by
cooling from above)
23
(No Transcript)
24
Cellular Convection
- Open vs. closed cells
- Wintertime cold air masses that advect from
continents out over warm ocean currents produce
convective marine PBLs. - Cold air masses that advect from continents out
over warm ocean currents produce convective
marine PBLs. - The convective cloudiness that evolves off-shore
occurs as bands or streets and gives way
downstream to chains of open cells and then
farther out to sea there are eventually patterns
of open and closed hexagonal convection
25
Cellular Convection
- Open vs. closed cells
- This is the natural order to expect as unstable
convective PBLs are growing and near steady-state
can develop in time with sufficient heating (and
farther out to sea, which also finds the
decreasing effects of vertical shear in the
horizontal wind (lt10-3s-1))
26
Cellular Convection
- Actinae spoke-like cellular convection formations
- Actinae do not occur in Type I CTBLs, because the
process is too dynamic. - Actinae only occur in Type II CTBLs. The reason
being that in the Rayleigh-Prandtl regime
stability diagram there is a very small space (a
narrow range of conditions that will support
actinae). - In the Type II case the atmosphere is functioning
in such a slow dynamic mode that the actinae can
be achieved. It is easy to produce the actinae
in the laboratory.
27
Cellular Convection
- Actinae spoke-like cellular convection formations
- The spoke-pattern convection is a geometric
plan-form that represents a transition between
the open and closed cellular convection
patterns. It is a transitional pattern and that
is why it is always found between regions of
open and closed cells. - In thermal convection (both theory and lab
results) you can develop 6-arm patterns (linear
mode for weakly supercritical Rayleigh) to
12-arm patterns (non-linear mode). - Rotation would be no surprise because background
vertical vorticity gets stretched and the
convective overturning (especially during
transition from open to closed structure)
produces horizontal vortex tubes as well.
28
Actinae