Lecture 7 Two-dimensional NMR

1
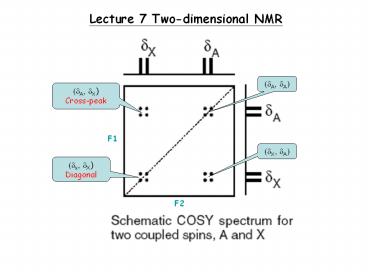
Lecture 7 Two-dimensional NMR
(?A, ?A)
(?A, ?X) Cross-peak
F1
(?X, ?A)
(?x, ?X) Diagonal
F2
2
Interpretation of peaks in 2D spectrum
Need mixing time to transfer magnetization to see
cross peaks !
3
Allows interaction to take place
1H excitation
General scheme
To keep track of 1H magnetization (Signal
not recorded)
Signal contains info due to the previous three
steps
t1 0
Experiment Get a series of FIDs with
incremental t1 by a time ?. Thus, for an expt
with n traces t1 For the traces will be 0, ?,
2?, 3?, 4? ----- (n-1)?, respectively. We will
obtain a series of n 1D FID of S1(t1, t2).
Fourier transform w.r.t. t2 will get a series of
n 1D spectra S2(t1, ?2). Further transform
w.r.t. t1 will get a 2D spectrum of S3(?1, ?2).
Spectral width in the t1 (F1) dimension will be
SW 1/?
F2 ?1
FT
FT
t1 ?
F2 ?2
t1 2?
F2 ?1
t1 3?
F2 ?3
t1 4?
F2 ?4
t1 5?
F2 ?N
t1 n?
4

• Review on product operator
  formalism
• 1. At thermal equilibrium I Iz
• 2. Effect of a pulse (Rotation)
• exp(-i?Ia)(old operator)exp(i?Ia) cos? (Old
  operator) sin? (new operator)
• 3. Evolution during t1
• (free precession) (rotation w.r.t. Z-axis)

- Iy for ?1tp 90o
Product operator for two spins Cannot be
treated by vector model Two pure spin states
I1x, I1y, I1z and I2x, I2y, I2z I1x and I2x are
two absorption mode signals and I1y and I2y are
two dispersion mode signals. These are all
observables (Classical vectors)
5
Coupled two spins Each spin splits into two spins
Anti-phase magnetization 2I1xI2z, 2I1yI2z,
2I1zI2x, 2I1zI2y (Single quantum
coherence) (Not observable)
Double quantum coherence 2I1xI2x, 2I1xI2y,
2I1yI2x, 2I1yI2y (Not observable) Zero quantum
coherence I1zI2z (Not directly
observable) Including an unit vector, E, there
are a total of 16 product operators in a
weakly-coupled two-spin system. Understand the
operation of these 16 operators is essential to
understand multi-dimensional NMR expts.
6
Example 1 Free precession of spin I1x of a
coupled two-spin system Hamiltonian Hfree
?1I1z ?2I2z

cos?1tI1x sin?1tI1y
No effect
Example 2 The evolution of 2I1xI2z under a 90o
pulse about the y-axis applied to both spins
Hamiltonian Hfree ?1I1y ?1I2y
7
Evolution under coupling Hamiltonian HJ
2?J12I1zI2z Causes inter-conversion of
in-phase and anti-phase magnetization according
to the Diagram, i.e. in-phase ? anti-phase and
anti-phase ? in-phase according to the rules
Must have only one component in the X-Y plane !!!
8

• Coherence order Only single quantum coherences
  are observables
• Single quantum coherences (p 1) Ix, Iy,
  2I1zI2y, I1yI2z, 2I1xI2z . etc
• Zero quantum coherence Iz, I1z2z
• Raising and lowering operators I ½(Ix
  iIy) I- 1/2 (Ix i-Iy)
• Coherence order of I is p 1 and that of
  I- is p -1
• Ix ½(I I-) Iy 1/2i (I - I-) are both
  mixed states contain order
• p 1 and p -1
• For the operator 2I1xI2x we have
• 2I1xI2x 2x ½(I1 I1-) x ½(I2 I2-)
  ½(I1I2 I1-I2-) ½(I1I2- I1-I2)

P 2
P -2
P 0
P 0
(Pure double quantum state)
(Pure zero quantum state)
9
2D-NOESY of two spins w/ no J-coupling

• Consider two non-J-coupled spin system
• Before pulse Itotal
• Let us focus on spin 1 first
• 2. 90o pulse (Rotation)

3. t1 evolution 4. Second 90o pulse 5.
Mixing time Only term with Iz can transfer
energy thru chemical exchange. Other terms
will be ignored. This term is frequency labelled
(Dep. on ?1 and t1). Assume a fraction of f
is lost due to exchange. Then after mixing time
(No relaxation)
6. Second 90o pulse
10
7. Detection during t2

• The y-magnetization
• Let A1(2) FTcos?1t2 is the absorption
  signal at ?1 in F2 and A2(2) FTos?2t2 as the
  absorption mode signal at ?2 in F2. Thus, the
  y-magnetization becomes
• Thus, FT w.r.t. t2 give two peaks at ?1 and ?2
  and the amplitudes of these two peaks are
  modulated by (1-f)cos?1t1 and fcos?1t1,
  respectively.
• FT w.r.t. t1 gives
  
• where A11 FTcos?t is the absorption mode
  signal at ?1 in F1.
• Starting from spin 1 we observe two peaks at
  (F1, F2) (?1, ?1) and (F1, F2) (?1, ?2)
• ? Similarly, if we start at spin 2 we will get
  another two peaks at (F1, F2) (?2, ?2) and
• (F1, F2) (?2, ?1)
• ? Thus, the final spectrum will contain four
  peaks at (F1, F2) (?1, ?1), (F1, F2) (?1,
  ?2),

(Diagonal)
(Cross peak)
11
Allows interaction to take place
1H excitation
General scheme
To keep track of 1H magnetization (Signal
not recorded)
Signal contains info due to the previous three
steps
Experiment Get a series of FIDs with
incremental t1 by a time ?. Thus, for an expt
with n traces t1 For the traces will be 0, ?,
2?, 3?, 4? ----- (n-1)?, respectively. We will
obtain a series of n 1D FID of S1(t1, t2).
Fourier transform w.r.t. t2 will get a series of
n 1D spectra S2(t1, ?2). Further transform
w.r.t. t1 will get a 2D spectrum of S3(?1, ?2).
Spectral width in the t1 (F1) dimension will be
SW 1/?
t1 0
F2 ?1
FT(t1)
FT(?)
t1 ?, cos?1?
F2 ?2
t1 2?, cos?12?
F2 ?1
t1 3?, cos?13?
F2 ?3
t1 4?, cos?14?
F2 ?4
t1 5?, cos?15?
cos?4?
FT
F2 ?N
t1 n?, cos?1n?
12
7.4. 2D experiments using coherence transfer
through J-coupling
7.4.1. COSY After 1st 90o pulse t1
evolution J-coupling Effect of the second
pulse
(p0, unobservable)
(p0 or 2) (unobservable)
(In-phase, dispersive)
(Anti-phase) (Single quantum coh.)
13
The third term can be rewritten as Thus, it
gives rise to two dispersive peaks at ?1 ?J12
in F1 dimension Similar behavior will be
observed in the F2 dimension, Thus it give a
double dispersive line shape as shown below.
The 4th term can be rewritten as Two
absorption peaks of opposite signs (anti-phase)
at ?1 ?J12 in F1 dimension will be observed.
14
Similar anti-phase behavior will be observed in
F2 dimension, thus multiplying F1 and F2
dimensions together we will observe the
characteristic anti-phase square array.
? Use double-quantum filtered COSY (DQF-COSY)
15
Double-quantum filtered-COSY (DQF-COSY) Using
phase cycling to select only the double quantum
term (2) can be converted to single quantum for
observation. (Thus, double quantum-filtered)
P 2
P -2
P 0
P 0
Rewrite the double quantum term as
The effect of the last 90o pulse
Anti-phase absorption diagonal peak
Anti-phase absorption cross peak
16
(No Transcript)
17
Heteronuclear correlation spectroscopy

• Heteronuclear Multiple Quantum Correlation
  (HMQC)
• For spin 1, the chemical shift evolution is
  totally refocused at the beginning of detection.
  So we need to analyze only the 13C part (spin 2)

J-coupling
J-coupling
After 90o 1H pulse
At the end of ? - I1y

2I1xI2z for ? 1/2J12 After 2nd 90o
pulse The above term contains both zero and
double quantum coherences. Multiple quantum
coherence is not affected by J coupling. Thus, we
need to consider only the chemical shift
evolution of spin 2.
J-coupling
13C evolution
J-coupling during 2nd ?
18
Phase cycling If the 1st 90o pulse is applied
alone X axis the final term will also change
sign. But those which are not bonded to 13C will
not be affected. Those do two expt with X- and
X-pulses alternating and subtract the signal
will remove unwanted signal. 2. Heteronuclear
Multiple-Bond Correlation (HMBC) In HMQC
optimal ? 1/2J 1/(2x140) 3.6 ms. In order
to detect long range coupling of smaller J one
needs to use longer ?, say 30-60 ms (For
detecting quaternary carbon which has no directly
bonded proton). ? Less sensitive due to
relaxation.
3. Heteronuclear Single Quantum Correlation (HSQC)

• Too complex to analyze in detail for every terms.
• Need intelligent analysis, i.e. focusing only
  on terms that lead to observables.

19
(No Transcript)
20
W/ or w/o DCPL
21
7.6 Lineshape and frequency discrimination
22
(No Transcript)