Daily Check - PowerPoint PPT Presentation
1 / 23
Title:
Daily Check
Description:
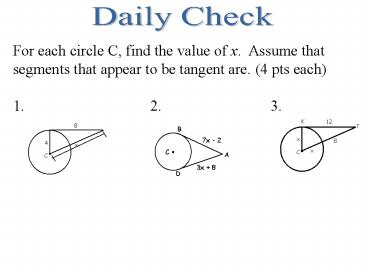
For each circle C, find the value of x. Assume that segments that appear to be tangent are. (4 pts each) 1. 2. 3. K 12 T x 8 x C c c b EOCT Practice Question of the ... – PowerPoint PPT presentation
Number of Views:76
Avg rating:3.0/5.0
Title: Daily Check
1
Daily Check
For each circle C, find the value of x. Assume
that segments that appear to be tangent are. (4
pts each) 1. 2. 3.
2
EOCT Practice 1
c
3
EOCT Practice 2
c
4
EOCT Practice 3
b
5
EOCT Practice
Question of the Day
6
Math IIDay 39 (10-6-10)
UNIT QUESTION What special properties are found
with the parts of a circle? Standard MM2G1,
MM2G2 Todays Question What effect does
changing the radius have on S.A. and Volume of a
sphere? Standard MM2G4.a,b
7
6.9 Surface Area of Spheres
8
Radius of a Sphere
r
9
If you cut a sphere right down the middle you
would create two congruent halves called
HEMISPHERES.
You can think of the globe. The equator cuts the
earth into the northern and southern hemisphere.
10
Look at the cross section formed when you cut a
sphere in half.
What shape is it?
A circle!!! This is called the GREAT CIRCLE of
the sphere.
11
Formulas for a Sphere
12
Surface Area of a Sphere (round to the nearest
hundredths)
8 in
13
Surface Area of a Sphere (round to the nearest
hundredths)
10 cm
14
The circumference of a great circle of a sphere
is 25 inches. Find the surface area of the
sphere. (Round to the nearest tenths.)
25 in
15
Surface Area of a Sphere A spherical balloon has
an initial radius of 5 in. When more air is
added, the radius becomes 10 in. Explain how the
S.A. changes as the radius changes.
10 in
5 in
16
6.9 Volume of Spheres
17
Volume of a Sphere (round to the nearest
hundredths)
2 cm
18
Volume of a Sphere
10 cm
19
Volume of a Sphere A spherical balloon has an
initial radius of 5 in. When more air is added,
the radius becomes 10 in. Explain how the volume
changes as the radius changes.
10 in
5 in
20
SA and Volume of a Sphere A spherical balloon has
a surface area of 16 in.2 Find the volume of the
sphere.
10 in
5 in
21
Volume of a Sphere A sphere has an initial volume
of 400 cm.3 The sphere is made bigger by making
the radius 4 times as big. What is the new
volume of the sphere?
10 in
5 in
22
Class work Test Prep Workbook Page 38
23
Homework Page 239 1-18




























![READ [PDF] Blood Pressure Log Book - Check My Engine: Blood Pressure J PowerPoint PPT Presentation](https://s3.amazonaws.com/images.powershow.com/10083521.th0.jpg?_=20240723039)

