Multiaxial Loading

1
Multiaxial Loading
2
How do we relate stress and strain?
3
Isotropy vs. Anisotropy
4
Multiaxial Hookes Law

• ?????x 1/E?xx - ?? ?yy ?zz )
• ?????y 1/E?yy - ?? ?xx ?zz )
• ?????z 1/E?zz - ?? ?yy ?xx )
• ?????xy ?xy/G
• ?????xz ?xz/G
• ?????yz ?yz/G

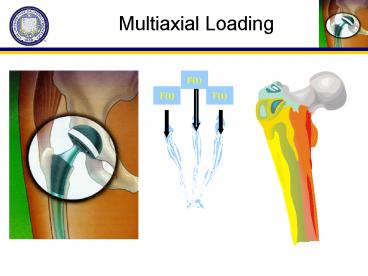
5
Example Multiaxial Loading in a glenoid component

• Consider the glenoid component of a shoulder
  implant that is subjected to axial loading
  (z-direction) but is confined against deformation
  in both the x and y directions.
• Assume that this device is loaded with a
  compressive stress ?zz 30 MPa. The bearing
  material is UHMWPE. Assume that the material is
  linear elastic and isotropic. The material
  properties are as follows E 1 GPa, ?yield 25
  MPa, ? 0.4.
• What stresses develop in the device?

6
Analysis
Strains in x and y directions are zero due to
constraint. Substitution leads to
20 MPa
7
Rule of Mixtures Bioactive glass coating

• A polymer sleeve with a bioactive glass coating
  is designed with an internal diameter equal to
  6-mm and an outer diameter equal to 12-mm.
• This type of device can be used to help with bone
  in-growth for a joint replacement. It is often
  desirable to design these sleeves to have a
  modulus similar to that of bone.
• We can use the rule-of-mixtures to design the
  composite cross-section, of only the polymer and
  bioactive glass, such that the axial modulus of
  this sleeve is equal to that of cortical bone.

8

• A schematic of the cross-section is shown below.
  Assume the following material properties
• E-polymer 10 GPaE-bioactive glass 27
  GPaE-cortical bone 17 GPa

bioactive glass
polymer
6 mm
12 mm
9
Analysis

• For this problem, the upper bound of modulus for
  the rule-of-mixtures can be assumed. The equation
  is given below

EEQUIV the equivalent modulus, you want this to
equal 17 GPa Apoly cross-sectional area of the
polymer Aglass cross-sectional area of the
bioactive glass The cross-sectional areas of the
polymer and bioactive glass are unknown.
10
Analysis cont.

• t thickness of the polymer (this is what you
  need to solve for)
• ri inner radius of the cross section 3mm, ro
  outer radius 6mm. Solve for t and simplify
  it to get a quadratic equation

t tpolymer 2mm. Then there is 1mm left over
for the bioactive glass (tbioactive glass 1mm).
11
Pressure vessels
12
Pressure vessel equations

• For a thin-walled spherical pressure vessel
• ?1 ?2 pr/2t
• For a thin-walled cylindrical pressure vessel
• ?1 pr/t, ?2 ?1 /2 pr/2t

13
Example

• A polymeric material is chosen for a balloon
  angioplasty procedure. The balloon is spherical
  and thin-walled. The diameter of the balloon is
  1.2 cm, with a wall thickness of 0.16mm. The
  balloon withstands an internal pressure of 0.7
  MPa. What stresses develop in the balloon?

14
Analysis

• ?1 ?2 pr/2t
• ? pr/2t (0.7MPa)(6mm)/(0.32mm) 13MPa