Aucun titre de diapositive - PowerPoint PPT Presentation
1 / 61
Title:
Aucun titre de diapositive
Description:
avec k = 3.E.I/L3. E,I. F. X. L. Raideurs. X. F= K.X. L. E, I. X. Due au moment ... Aucun dommage. B timents peu lev s. Peu de d g ts. B timents de 10 30 tages. Beaucoup de ... – PowerPoint PPT presentation
Number of Views:64
Avg rating:3.0/5.0
Title: Aucun titre de diapositive
1
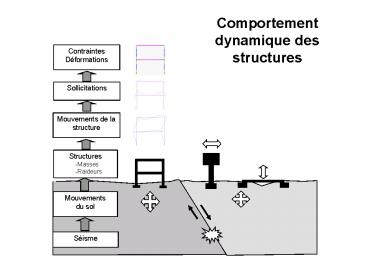
Comportement dynamique des structures
Mouvements du sol
Séisme
2
- Séisme
- magnitude
- intensité
- mécanisme au foyer
- Structures
- Masses
- Raideurs
- Matériaux
- Mouvements du sol
- accélérogrammes
- Spectres de Fourier
- Spectres de réponses
3
Masses
4
Rigidité/ déformabilité
- F k.X ? k F/X
- F N Force
- X m déplacement
- k N/m raideur
5
Raideurs
X
6
(No Transcript)
7
Exemples de raideurs de qq. structures
élémentaires
k n.E.I/L3 avec k MN/m raideur de
la structure n - coefficient fonction de la
nature des liaisons E MPa module dYoung du
matériau I m4 inertie des sections L
m longueur de lélément
H hauteur poteaux L portée de la poutre I moment
quadratique ? (Ipoutre.H/Ipoteau.L) a
(16?)/(46?)
8
Matériaux Lois de comportement
?
2.10-3 3,5.10-3
9
Comportement sur un cycle de chargement
10
Sollicitations cycliques
11
Sollicitations cycliquesDaprès
Krawinkler-Bertero-Popov Priesley
12
Analyse modale
- Etude de loscillateur simple
13
- Etude dynamique
14
Y
X
Xsol
X
Principe fondamental de la
dynamique SFe m.a force de
rappel force damortissement force dinertie
- kx - cx m (xxsol)
(en projection sur X)
15
Oscillations libres, amorties F(inertie)
F(rappel) F(amortissement) 0 ? m.x
kx cx 0
Oscillations forcées (séisme), amorties
F(inertie) F(rappel) F(amortissement) F
? m.x kx cx -m.xsol
16
Analyse modale recherche du (ou des) mode
propre de vibration (T, f, ?)
17
PERIODES
18
Amortissement dissipation dénergie sismique
19
Oscillations libres pour différents facteurs
damortissement
20
Quelques valeurs du facteur d amortissement...
21
Fonction de k et X
Energie potentielle
Fonction de c et x'
Energie cinétique
Esismique Epotentielle Ecinétique Edissipée
Energie dissipée
Communiquée à la structure par les mouvements du
sol
Fonction de m et v
Energie sismique
22
Conception des structures
- Augmenter le stockage d'énergie Augmenter la
résistance mécanique dans le domaine élastique
Energie mécanique stockée (potentielle et
cinétique)
Augmenter la dissipation d'énergie Augmenter
l'amortissement externe ou interne
(plastification de matériaux)
Energie dissipée
Minimiser les forces d'inertie Diminuer la
masse Diminuer l'accélération réponse (modifier
les raideurs)
Energie sismique
23
Analyse spectralerecherche de la réponse de la
structure (accélération, vitesse ou déplacement)
par la méthode des spectres
24
Pont de Tacoma (Californie)
Passerelle Eole (Brest)
Vidéo Mur Marseille
25
(No Transcript)
26
Réponse de la structure
déplacement maximum
accélération maximum
27
(No Transcript)
28
Utilisation du spectre de réponse en accélération
d un séisme
T1 0 T2
T3
T4 Structure très raide Structure raide
Structure souple Structure très souple
T1 T2 T3
T4
29
Masses
30
Liaisons
Sections
Matériaux
hauteurs
31
Spectre de réponse dun bâtiment à un étage
soumis à un mouvement périodique
5
0
4
0,1
3
Facteur damortissement
0,2
Déplacement bâtiment /Amplitude des mouvements du
sol
2
0,5
1
1
4
3
1
2
Tbâtiment/Texcitation
32
Northridge 94
33
Spectres de réponse
34
spectre de dimensionnement réglementaire
35
170 cm/s²
T 2s
MEXICO 1985
35 cm/s²
T 2s
150 cm/s²
36
a (g)
T N/10
0.75g
MEXICO1985
x 7.7
0.15g
x 5
0.035g
T (s)
37
MEXICO 1985
Tour Latino Américaine de 50 étages Aucun dommage
Bâtiments de 10 à 30 étages Beaucoup de
destructions
Bâtiments peu élevés Peu de dégâts
38
Effet de site Mexico (1985)
39
Comparaison daccélérogrammes et de spectres de
réponse
40
(No Transcript)
41
(No Transcript)
42
Microzonage de Fort de France
Carte des Effets de Site
43
BRGM, 1996
Microzonage de Fort-de-France effets de site.
Chaque spectre de couleur correspond à une zone
de la carte précédente.
44
Séisme
m.x kx cx f(t)
45
Exemple 1 Château deauModélisation
M 150 tonnes
K 3EI/L3
15 m
46
Château deau Masse, Raideur
M 150 tonnes
K 3EI/L3 17,1 MN/m avec L 15 m E Eij
11000.fcj1/3 11000.251/3 32164 MPa I ?.(D4
- d4)/64 ?.(24-1,44)/64 0,597 m4
47
Analyse modale
T 2. ?.(M/k)1/2
T 2. ?.(150000/17,1.106)1/2 T 0,59 s
Analyse spectrale
3,86
0,59
48
Force sismique, déplacement
F M.a F 150000.3,86 F 580 000 N F 0,58
MN
49
Exemple 2Bâtiment sur poteaux
50
Modélisation
- Dans le sens X
- Dalle diaphragme rigide
- Masse concentrée dans la dalle
- Oscillateur simple
- Raideur
- k raideur des 10 poteaux
51
Analyse modale
- M G0,25Q 274000 kg
- k 10x3EI/l3 si les poteaux sont encastrés en
pied et articulés en tête - E 11000.(25)1/3 32160 MPa
- I b.h3/12 0,002133 m4
- h 4,25 m
- k 10x3x32160x0,002133/4,253 26,82 MN/m
52
Analyse spectrale
- Force sismique totale
- F 0,271x3,69 1 MN
- Chaque poteau reprend la même charge
- soit 1/10 0,1 MN.
- Déplacement maxi
- X F/k 0,1/26,82 0,037m
F m.a
Période T
53
Exemple 3 Etude dun pont
X
Culées enterrées
54
X
Etude vis-à-vis des 3 composantes de laction
sismique
Y
Z
55
4 appuis néoprène
17m
2 butées transversales
12m
0,6m
Chevêtre
56
Modélisation
57
Analyse modale
58
a(T) m/s2
Spectre de réponse en accélération
6,75
4,05./T
T s
0,6
59
Analyse spectrale
a(T) m/s2
ay az 6,75
4,05./T
ax 4,95
0,6
T s
Ty 0
Tz 0,31
Tx 0,82
Spectre de réponse en accélération
60
Analyse spectrale
61
Remarques sur la discrétisation des masses