Diapositiva 1

1
(No Transcript)
2
(No Transcript)
3
(No Transcript)
4
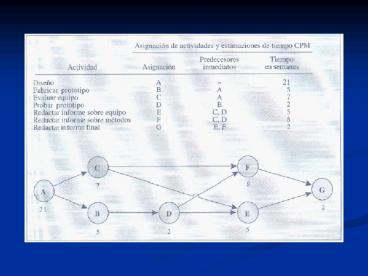
CPM con tres estimaciones de tiempo para las
actividades Si no resulta confiable una sola
estimación del tiempo requerido para terminar una
actividad, lo mejor es utilizar tres estimaciones
de tiempos. Estos tres tiempos no sólo permiten
calcular el tiempo de la actividad, sino que
permiten obtener una estimación de probabilidad
para el tiempo de terminación correspondiente a
toda la red. En síntesis, el procedimiento es el
siguiente El tiempo de actividad calculado es
un promedio ponderado, con más peso asignado a la
estimación mejor y menos a los tiempos máximo y
mínimo. La relación que se suele utilizar es 4,
1, 1, como se verá más adelante. El tiempo de
terminación calculado para la red se computa
mediante estadísticas básicas, que estipulan que
la desviación estándar de una secuencia de
eventos es la raíz cuadrada de la suma de las
variaciones de cada evento. Ésta es la lógica de
Z, que aparece en el paso 7 a continuación.
Luego, al simplemente ubicar Z (el número de
desviaciones estándar) en una tabla de
probabilidades (como en el anexo D), se obtiene
la probabilidad de terminación.
5

• Solución
• Identifique cada una de las actividades que se
  deben realizar en el proyecto.
• 2. Determine la secuencia de actividades y
  construya una red que refleje las relaciones de
  precedencia.
• 3. Las tres estimaciones para un tiempo de
  actividad son
• a Tiempo optimista el período mínimo razonable
  en el que se puede terminar la actividad. (Sólo
  existe una pequeña probabilidad, que por lo
  general se considera 1 , de que la actividad se
  pueda terminar en menos tiempo).
• m Tiempo más probable la mejor aproximación
  del tiempo requerido. Como m sería el tiempo que
  se cree que aparecerá con mayor probabilidad,
  también es el modo de la distribución beta que se
  explica en el paso 4.
• b Tiempo pesimista el periodo máximo razonable
  en el que se terminaría la actividad. (Sólo
  existe una pequeña probabilidad, que por lo
  general se considera en un 1 , de que la
  actividad se demore más tiempo).
• Por lo general, esta información se obtiene de
  las personas que van a realizar la actividad.

6
4. Calcule el tiempo anticipado, o expected time
(ET), para cada actividad. La fórmula para
efectuar este cálculo es a 4m b ET
------------------ 6 Esto se basa en
la distribución estadística beta y le asigna al
tiempo más probable (m) un peso cuatro veces
mayor que el del tiempo optimista (a) o el del
tiempo pesimista (b). La distribución beta es
extremadamente flexible puede asumir la variedad
de formas que suelen surgir, tiene puntos finales
finitos (lo que limita los tiempos de actividad
posibles al área entre a y b) y, en la versión
simplificada, permite la computación directa de
la media de actividad y la desviación
estándar. 5. Determine la ruta crítica.
Utilizando los tiempos anticipados, se calcula
una ruta crítica de la misma manera que en el
caso de una sola estimación de tiempo. 6.
Calcule las variaciones (?2) de los tiempos de
actividad. Específicamente, esta es la variación
?2, asociada con cada ET, y se computa de la
siguiente manera
7
Como se puede ver, la variación es el cuadrado de
un sexto de la diferencia entre las dos
estimaciones de tiempo extremas. Desde luego,
cuanto mayor sea esta diferencia, mayor será la
variación. 7. Determine la probabilidad de
terminar el proyecto en una fecha establecida. Un
aspecto valioso del uso de tres estimaciones de
tiempo es que permite al analista evaluar el
efecto de la incertidumbre en el tiempo de
terminación del proyecto. La mecánica para
calcular esta probabilidad es la siguiente a.
Sume los valores de variación asociados con cada
actividad de la ruta crítica. (Para casos en que
exista más de una ruta crítica, vea el siguiente
ejemplo.) b. Sustituya esta cifra, junto con la
fecha de vencimiento del proyecto y el tiempo
anticipado de terminación del mismo, en la
fórmula de transformación Z. Esta fórmula es
8
D Fecha de terminación deseada del proyecto TE
Tiempo de terminación esperado del
proyecto ??2cp Suma de las variaciones en la
ruta crítica c. Calcule el valor de Z, que es
el número de desviaciones estándar de la fecha de
vencimiento del proyecto con respecto al tiempo
de terminación esperado. d. Utilizando el valor
de Z, determine la probabilidad de cumplir con la
fecha de vencimiento del proyecto (utilizando
una tabla de probabilidades normales, como el
anexo E). El tiempo de terminación esperado es
el tiempo de inicio más la suma de tiempos de
actividad en la ruta crítica.
9
(No Transcript)
10
Como hay dos caminos críticos en la red, hay que
decidir qué variaciones utilizar para contar con
la probabilidad de cumplir con la fecha de
vencimiento del proyecto. Un método conservador
aconseja utilizar el camino con la variación
total más grande, pues esto concentraría la
atención de la gerencia en las actividades que
con más probabilidad exhibirán grandes
variaciones. Con base en esto, las variaciones
relacionadas con las actividades A, C, F y G se
utilizarían para determinar la probabilidad de
terminación. Así, ??2cp 9 2 7/9 1/9 O
11.89. Suponga que la gerencia pide la
probabilidad de completar el proyecto en 35
semanas. En ese caso, D es 35. El tiempo
esperado de terminación se determinó como 38.
Sustituyendo Z en la ecuación y resolviéndola, se
obtiene En el anexo D se observa que un valor
Z de -0.87 da una probabilidad de 0.19, lo cual
significa que el gerente de proyecto sólo tiene
aproximadamente un 19 de probabilidades de
completar el proyecto en 35 semanas. Se debe
tener en cuenta que esta probabilidad en realidad
es aquella de completar la ruta crítica ACEG.
Como existe otra ruta crítica y otras rutas que
podrían volverse críticas, la probabilidad de
terminar el proyecto en 35 semanas en realidad es
de menos de 19.
11
(No Transcript)
12
(No Transcript)
13
(No Transcript)
14
(No Transcript)