Sinusoidal Models (modeling with the sine/cosine functions)

1
Sinusoidal Models(modeling with the sine/cosine
functions)
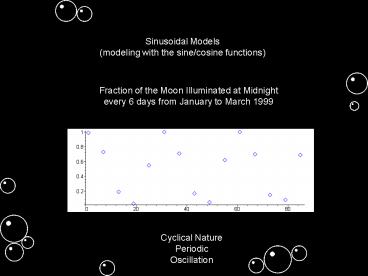
Fraction of the Moon Illuminated at
Midnightevery 6 days from January to March 1999
Cyclical NaturePeriodicOscillation
2
Sinusoidal Models(modeling with the sine/cosine
functions)
To use sine and cosine functions for modeling, we
must be able to
stretch them up and squash them down
y ksin(x)
pull them out and squeeze them together
y sin(kx)
move them up and move them down
y sin(x) k
move them left and move them right
y sin(x-k)
3
stretch them up and squash them down
y Asin(x)
y 1sin(x)Period 2pMidline y 0Amplitude 1
4
stretch them up and squash them down
y Asin(x)
y 1sin(x)Period 2pMidline y 0Amplitude 1
y 3sin(x)Period 2pMidline y 0Amplitude 2
5
stretch them up and squash them down
y Asin(x)
y 1sin(x)Period 2pMidline y 0Amplitude 1
y 3sin(x)Period 2pMidline y 0Amplitude 2
y -0.5sin(x)Period 2pMidline y
0Amplitude 0.5
6
Sinusoidal Models(modeling with the sine/cosine
functions)
In the formula f(x) Asin(x), A is the amplitude
of the sine curve.
7
pull them out and squeeze them together
y sin(Bx)
y sin(1x)Period 2pMidline y 0Amplitude 1
8
pull them out and squeeze them together
y sin(Bx)
y 1sin(x)Period 2pMidline y 0Amplitude 1
y sin(4x)Period p/2Midline y 0Amplitude
1
9
pull them out and squeeze them together
y sin(Bx)
y 1sin(x)Period 2pMidline y 0Amplitude 1
y sin(4x)Period p/2Midline y 0Amplitude
1
y sin(0.5x)Period 4pMidline y
0Amplitude 1
10
Sinusoidal Models(modeling with the sine/cosine
functions)
In the formula f(x) Asin(x), the amplitude of
the curve is A.
In the formula f(x) sin(Bx), the period of the
curve is 2p/B.
11
move them up and move them down
y sin(x) D
y sin(x)Period 2pMidline y 0Amplitude 1
y sin(x)2Period 2pMidline y 2Amplitude
1
y sin(x)-1Period 2pMidline y
-1Amplitude 1
12
Sinusoidal Models(modeling with the sine/cosine
functions)
In the formula f(x) Asin(x), the amplitude of
the curve is A.
In the formula f(x) sin(Bx), the period of the
curve is 2p/B.
In the formula f(x) sin(x) D, the midline of
the curve is y D .
13
move them left and move them right
y sin(x-C)
y sin(x)Period 2pMidline y 0Amplitude
1Phase Shift none
y sin(xp/2)Period 2pMidline y
0Amplitude 1Phase Shift -p/2
y sin(x-p)Period 2pMidline y 0Amplitude
1Phase Shift p
14
Sinusoidal Models(modeling with the sine/cosine
functions)
In the formula f(x) Asin(x), the amplitude of
the curve is A.
In the formula f(x) sin(Bx), the period of the
curve is 2p/B.
In the formula f(x) sin(x) D, the midline of
the curve is y D .
In the formula f(x) sin(x-C), the phase shift
of the curve is C
15
Sinusoidal Models(modeling with the sine/cosine
functions)
f(x) Asin(B(x-C)) D
The amplitude of the curve is A.
The period of the curve is 2p/B.
The midline of the curve is y D .
The phase shift of the curve is C.
CYU 6.8/311
16
5/311
f(t) sin(t)
f(t) sin(3t)
f(t) sin(3t p/4)
17
67/311
f(t) -3sin(0.5t)
f(t) -3sin(0.5(t1))
f(t) -3sin(0.5t1)
18
Sinusoidal Models(modeling with the sine/cosine
functions)
f(x) Asin(B(x-C)) D
The amplitude of the curve is A.
The period of the curve is 2p/B.
The midline of the curve is y D .
The phase shift of the curve is C.
More Practice 31, 33, 41, 43, 45
19
More Practice 31, 33, 41, 43, 45
31/329 amplitude 3, period p/4, vertical shift
2 down
f(x) 3sin(8x) - 2
by hand graph
Maple graph
20
More Practice 31, 33, 41, 43, 45
33/329 amplitude 1, period 6, horizontal shift 2
left
by hand graph
Maple graph
21
More Practice 31, 33, 41, 43, 45
41/330 write a sine or cosine formula that could
represent the given graph
22
More Practice 31, 33, 41, 43, 45
43/330 write a sine or cosine formula that could
represent the given graph
23
More Practice 31, 33, 41, 43, 45
45/330 write a sine or cosine formula that could
represent the given graph
24
Homework
page328 31-35, 41-46 TURN IN 32, 34, 42,
44, 46 Check your formulas using a Maple graph.
25
Fraction of the Moon Illuminated at
Midnightevery 6 days from January to March 1999
Period is 30, so B p/15Midline is y
0.5Amplitude is 0.5. m(t) 0.5sin(p/15(t-C))0.
5 use graph to determine C
26
Fraction of the Moon Illuminated at
Midnightevery 6 days from January to March 1999
Period is 30, so B p/15Midline is y
0.5Amplitude is 0.5. m(t) 0.5sin(p/15(t-C))0.
5 use graph to determine C
27
Fraction of the Moon Illuminated at
Midnightevery 6 days from January to March 1999
Period is 30, so B p/15Midline is y
0.5Amplitude is 0.5. C is 6 units left m(t)
0.5sin(p/15(t-6))0.5