Solve a multistep problem

1
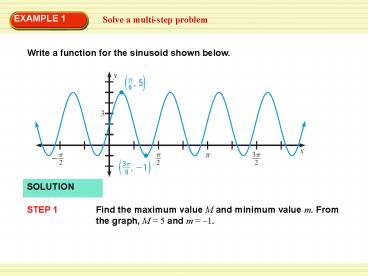
EXAMPLE 1
Solve a multi-step problem
SOLUTION
STEP 1
Find the maximum value M and minimum value m.
From the graph, M 5 and m 1.
2
EXAMPLE 1
Solve a multi-step problem
STEP 2
Identify the vertical shift, k. The value of k is
the mean of the maximum and minimum values. The
vertical shift is
So, k 2.
STEP 3
Decide whether the graph should be modeled by a
sine or cosine function. Because the graph
crosses the midline y 2 on the y-axis, the
graph is a sine curve with no horizontal shift.
So, h 0.
STEP 4
Find the amplitude and period. The period is
So, b 4.
3
EXAMPLE 1
Solve a multi-step problem
3.
The amplitude is
The graph is not a reflection, so a gt 0.
a 3.
Therefore,
4
EXAMPLE 2
Model circular motion
5
EXAMPLE 2
Model circular motion
SOLUTION
STEP 1
Find the maximum and minimum values of the
function. A ropes maximum height is 75 inches,
so M 75. A ropes minimum height is 3 inches,
so m 3.
6
EXAMPLE 2
Model circular motion
STEP 2
Identify the vertical shift. The vertical shift
for the model is
39
STEP 3
Decide whether the height should be modeled by a
sine or cosine function. When t 0, the height
is at its minimum. So, use a cosine function
whose graph is a reflection in the x-axis with no
horizontal shift (h 0).
7
EXAMPLE 2
Model circular motion
STEP 4
Find the amplitude and period.
The amplitude is
36.
Because the graph is a reflection, a lt 0. So, a
36. Because a rope is rotating at a rate of 2
revolutions per second, one revolution is
completed in 0.5 second. So, the period is
8
for Examples 1 and 2
GUIDED PRACTICE
Write a function for the sinusoid.
SOLUTION
STEP 1
Find the maximum value M and minimum value m.
From the graph, M 2 and m 2.
9
for Examples 1 and 2
GUIDED PRACTICE
STEP 2
Identify the vertical shift, k. The value of k is
the mean of the maximum and minimum values. The
vertical shift is
So, k 0.
10
for Examples 1 and 2
GUIDED PRACTICE
STEP 3
Decide whether the graph should be modeled by a
sine or cosine function. Because the graph peaks
at y 2 on the y-axis, the graph is a cos curve
with no horizontal shift. So, h 0.
STEP 4
Find the amplitude and period. The period is
So, b 3.
11
for Examples 1 and 2
GUIDED PRACTICE
2.
The amplitude is
The graph is not a reflection, so a gt 0.
a 2.
Therefore,
12
for Examples 1 and 2
GUIDED PRACTICE
Write a function for the sinusoid.
13
for Examples 1 and 2
GUIDED PRACTICE
3. WHAT IF? Describe how the model in Example 2
would change if the lowest point of a rope
is 5 inches above the ground and the
highest point is 70 inches above the ground.