Lesson 9: Primes and Division - PowerPoint PPT Presentation
1 / 23
Title:
Lesson 9: Primes and Division
Description:
Prime Factorization. If n is a composite integer, then n has a ... GCD and LCM using Prime Factorization. GCD of (a,b) = p1min(a1,b1) p2min(a2,b2) p3min(a3,b3) ... – PowerPoint PPT presentation
Number of Views:57
Avg rating:3.0/5.0
Title: Lesson 9: Primes and Division
1
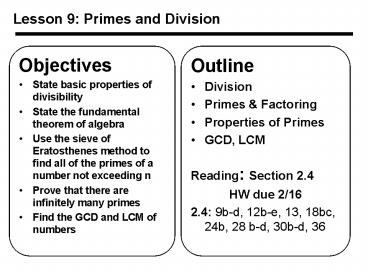
Lesson 9 Primes and Division
- Objectives
- State basic properties of divisibility
- State the fundamental theorem of algebra
- Use the sieve of Eratosthenes method to find all
of the primes of a number not exceeding n - Prove that there are infinitely many primes
- Find the GCD and LCM of numbers
- Outline
- Division
- Primes Factoring
- Properties of Primes
- GCD, LCM
- Reading Section 2.4
- HW due 2/16
- 2.4 9b-d, 12b-e, 13, 18bc, 24b, 28 b-d, 30b-d,
36
2
Ackermans Function
- http//www.kosara.net/thoughts/ackermann.html
3
Divisibility
- a divides b if there is an integer c such that
- b ac
- a is a factor of b
- b is a multiple of a (the cth multiple of a)
- a b
- If a does not divide b, we say
- a ?b
- a b if ?c(acb)
- universe of discourse integers
4
Divisibility
- 4 15
- 4 16
- 16 4
- 3 0
- 13 13
5
In Class
- Write down as many properties of divisibility as
you can think of. - (dont look ahead in the notes!!)
6
Divisibility Properties
- if a b and a c, then a (b c)
- if a b, then a bc for all integers c
- if a b and b c, then a c
7
Divisibility Properties
- If a, b, c are integers such that a b and a
c, then - a mb nc (m, n ? Z)
8
Prime Numbers
- A positive number greater than 1 is prime if and
only if the only positive factors of p are 1 and
p - non-primes are called composite
- How to test if a number is prime?
9
Fundamental Theorem of Arithmetic
- Every positive integer greater than 1 can be
written uniquely as a prime or as the product of
two or more primes where the prime factors are
written in order of nondecreasing size. - 64 222222
- 33 3 11
- 175 5 5 7
- 4951 4951
10
Prime Factorization
- 462
- 135
- 735
- 768
11
Prime Factorization
- If n is a composite integer, then n has a prime
divisor less than or equal to - Prove that 379 is prime
12
The Sieve of Eratosthenes
- The composites less than 121 must have prime
factors less than or equal to 11
13
Infinitude of Primes
- There are infinitely many primes
14
Mersenne Primes
- Mersenne primes are of the form 2p-1, where p is
prime - The largest known primes are Mersenne Primes
- Lucas-Lehmer test
- Great International Mersenne Prime Search (GIMPS)
- 2(13466917)-1 (over 4 million digits)
- http//www.isthe.com/chongo/tech/math/prime/mersen
ne.htmlM13466917
15
Distribution of Primes
- The number of primes not exceeding x approaches
ln(x) as x approaches infinity - If you randomly choose a number from 1, 106,
what is the probability that the number will be
prime?
16
Division
- Divisor
- Dividend
- Quotient
- Remainder
- q a/d
- q a div d
- r a mod d
17
Greatest Common Divisor
- If a,b are integers, gcd(a,b) is the largest
integer d such that d a and d b. - d is called the greatest common divisor of b and
a - In-Class
- gcd(63,27)
- gcd(49, 32)
- gcd(14, 18)
- If gcd(a,b) 1, then a,b are relatively prime
- Groups of numbers can be pairwise relatively
prime
18
Least Common Multiple
- lcm(a,b) is the smallest positive integer that is
divisible by both a and b - lcm(40, 50)
- lcm(133, 233)
- lcm(5, 50)
19
GCD and LCM using Prime Factorization
- GCD of (a,b) p1min(a1,b1) p2min(a2,b2)
p3min(a3,b3) - GCD (140, 400)
- LCM of (a,b) p1max(a1,b1) p2max(a2,b2)
p3max(a3,b3) - LCM (1000, 625)
20
Congruences
- a is congruent to b (modulo m) if m (a-b)
- a ? b (mod m)
- 14 ? 2 (mod 3)
- 27 ? 7 (mod 5)
- 25 ? 2 (mod 6)
21
Congruences
- 26 16 (mod 3)
- 15 13 (mod 2)
- 100 50 (mod 25)
- a ? b (mod m) if and only if (a mod m) (b mod
m) - a, b are congruent modulo m if and only if there
is an integer k such that (a b km)
22
Hashing
- Hashing functions map many-to-few
- h(k) k mod m
- (where k is number of keys and m is number of
slots)
23
Pseudorandom Number generation
- modulus m
- multiplier a (greater or equal to 2, less than
m) - increment c (greater or equal to 0, less than m)
- seed x0 (greater or equal to 0, less than m)
- xn1 (axn c) mod m
- Find sequence for m 7, a 5, c 1, x0 2