Collective Flow radial and anisotropic - PowerPoint PPT Presentation
1 / 32
Title:
Collective Flow radial and anisotropic
Description:
Life time: K(892) = 4 fm/c. L(1520) = 13 fm/c ... 'Life-time' between freeze-outs = 3-5 fm/c Partonic ' life-time' = 5-7 fm/c. Medium in d Au ? ... – PowerPoint PPT presentation
Number of Views:48
Avg rating:3.0/5.0
Title: Collective Flow radial and anisotropic
1
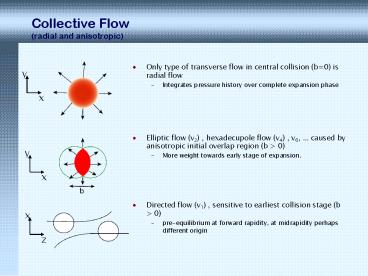
Collective Flow (radial and anisotropic)
- Only type of transverse flow in central collision
(b0) is radial flow - Integrates pressure history over complete
expansion phase
- Elliptic flow (v2) , hexadecupole flow (v4) , v6,
caused by anisotropic initial overlap region (b
gt 0) - More weight towards early stage of expansion.
- Directed flow (v1) , sensitive to earliest
collision stage (b gt 0) - pre-equilibrium at forward rapidity, at
midrapidity perhaps different origin
2
Azimuthal anisotropy Directed/Elliptic Flow
vn (n1,2) strength of directed/elliptic flow ?
azimuthal angle of detected particles ?
azimuthal angle of reaction plane
3
StrangenessProductionand Resonances
4
Strangeness Production
Tc ms
5
Strangeness enhancement
Strange particles with charged decay modes
- General arguments for enhancement
- 1. Lower energy threshold
- TQGP gt TC ms 150 MeV
- Note that strangeness is conserved in the
- strong interaction
- 2. Larger production cross-section
Enhancement is expected to be more pronounced for
multi-strange baryons and their anti-particles
6
Strangeness enhancement?
- Canonical (small system)
- Computed taking into account energy to create
companion to ensure conservation of strangeness.
Quantum Numbers conserved exactly. - Grand Canonical limit (large system)
- Just account for creation of particle itself.
The rest of the system acts as a reservoir and
picks up the slack. Quantum Numbers conserved
on average via chemical potential
- Phase space suppression of strangeness in
- small system/low temperature
- canonical suppression
- increases with strangeness
- decreases with volume
- observed enhancements
- Hamieh et al. Phys. Lett. B486 (2000) 61
7
Grand canonical applicable at RHIC?
130 GeV
- See drop in enhancement at higher energy
- Enhancement values as predicted by model
- Correlation volume not well modeled by Npart
System is in G.C. state for most central data
8
Strangeness saturation factor gs
9
Strangeness over nonstrangess
10
A theoretical view of the collision
Chemical freezeout (Tch ? Tc) inelastic
scattering stops
11
Strangeness enhancement
Strange particles with charged decay modes
- General arguments for enhancement
- 1. Lower energy threshold
- TQGP gt TC ms 150 MeV
- Note that strangeness is conserved in the
- strong interaction
- 2. Larger production cross-section
- 3. Pauli blocking (finite chemical potential)
Enhancement is expected to be more pronounced for
multi-strange baryons and their anti-particles
12
Strangeness Conservation
In Strong Interaction strange quarks can only
be produced in pairs !
Associated Production p N ? NLK
Pair Production p N ?pNKK-
Threshold in fixed target s (EmN)2 p2
Associated Production More Effective (lower
Threshold) _at_ low beam energies
13
K-/K Ratio from SIS up to RHIC
K
K -
14
Ratios that constrain model parameters
15
Chemical freeze-out Tempoerature
J. Cleymans and K. Redlich, PRL 81 (1998) 5284
16
Models to evaluate Tch and ?B
Particle density of each particle
- Statistical Thermal Model
- F. Becattini P. Braun-Munzinger, J. Stachel, D.
Magestro - J.Rafelski PLB(1991)333 J.Sollfrank et al.
PRC59(1999)1637 - Assume
- Ideal hadron resonance gas
- thermally and chemically equilibrated fireball
at hadro-chemical freeze-out - Recipe
- GRAND CANONICAL ensemble to describe partition
function ? density of particles of species ?i - fixed by constraints Volume V, , strangeness
chemical potential ?S, isospin - input measured particle ratios
- output temperature T and baryo-chemical
potential ?B
Qi 1 for u and d, -1 for ?u and ?d si 1 for
s, -1 for ?s gi spin-isospin freedom mi
particle mass Tch Chemical freeze-out
temperature mq light-quark chemical
potential ms strangeness chemical
potential gs strangeness saturation factor
Compare particle ratios to experimental data
17
Thermal model fit to data
- Particle ratios well described
- Tch 160 ? 5 MeV
- mB 24 ? 5 MeV
- ms 1.4 ?1.4 MeV
- gs 0.99 ?0.07
Data Fit (s) Ratio
Created a Large System in Local Chemical
Equilibrium
18
Tch systematics
- Hagedorn (1964)
- if the resonance mass spectrum grows
exponentially - (and this seems to be the case)
- there is a maximum possible temperature for a
system of hadrons
Blue Exp. fit Tc 158 MeV
r(m) (GeV-1)
filled AA open elementary
Green - 1411 states of 1967 Red 4627 states of
1996
m
Satz Nucl.Phys. A715 (2003) 3c
Seems he was correct cant seem to get above
Tch 170MeV
19
A theoretical view of the collision
2
Chemical freezeout (Tch ) 170 MeV Time between
Tch and Tfo
20
Resonance in Hadronic Medium
Life-time fm/c K(892) 4.0 S(1385)
5.7 L(1520) 13 ? (1020)
44
Size of medium AuAu , pp, dAu
collisions Centrality and energy dependence
Observables mass, width, pT spectrum,
yield Influence of medium hadronic vs leptonic
decay
21
Hadronic Re-scattering and Regeneration
Life-time fm/c r 1.3 ?
1.7 K(892) 4.0 S(1385)
5.7 L(1520) 13 ? (1020) 45
- Depends on
- hadronic phase density
- hadronic phase lifetime
22
Resonance Reconstruction in STAR
STAR Experiment
End view STAR TPC
Energy loss in TPC dE/dx
p
dE/dx
K
?
e
momentum GeV/c
- Identify decay candidates
- (p, dedx, E)
- Calculate invariant mass
K(892) ? ? K ? (1020) ? K K ?(1520) ?
p K S(1385) ? L p X(1530) ? X p
23
L(1520) Invariant Mass Reconstruction x
STAR Experiment
Phys. Rev. Lett. 97 (2006) 132301 e-Print
Archive nucl-ex/0604019 Ludovic Gaudichet
- Breit-Wigner-fit
- m 1516 ? 2 MeV/c2
- 12 ? 6 MeV/c2
- pdg
- 1519.5 ? 1.0 MeV/c2
- 15.6 ? 1.0 MeV/c2
Mixing categories reaction plane,
multiplicity, vertex position
24
Resonance Signals in pp and AuAu collisions
from STAR
pp
pp
AuAu
?(1020)
K(892)
AuAu
Masses and width are in agreement with PDG
D
?
?(1385)
AuAu
pp
pp
25
Momentum Spectra
K(892)
S(1385) and L(1520)
Integrated momentum distribution ? yields
26
Interactions of Resonance in Hadronic Nuclear
Medium
Life-time fm/c K(892) 4.0 S(1385)
5.7 L(1520) 13 ? (1020)
44
Phys. Rev. Lett. 97 (2006) 132301 e-Print
Archive nucl-ex/0604019
K and L show rescattering S shows
regeneration Regeneration/Rescattering cross
section s(Kp) lt s (Kp) lt s (Lp) ? L
K S
1 P. Braun-Munzinger et.al.,PLB 518(2001) 41,
priv. communication 2 Marcus Bleicher and
Jörg Aichelin Phys. Lett. B530 (2002) 81.
M. Bleicher and Horst Stöcker J.
Phys.G30 (2004) 111.
27
Temperature, Lifetime and Centrality Dependence
from L(1520)/L and K(892)/K x
- Model includes
- Temperature at chemical freeze-out
- Lifetime between chemical and
- thermal freeze-out
- By comparing two particle ratios
- (no regeneration)
- results between
- T 160 MeV, ?? 3 -5 fm/c
Life time K(892) 4 fm/c L(1520) 13 fm/c
C. Markert, G. Torrieri, J. Rafelski,
hep-ph/0206260
28
Lifetime of Heavy Ion Reaction
Kinetic freeze-out radius from two particle
correlation HBT
pT (GeV/c)
- Good agreement with hydrodynamic prediction at
RHIC - RHIC Tth 100 MeV, ? bT ? 0.55 c
DRlong bT ?Dt ?Dt 10 fm/c Dt lifetime of
the source
29
Lifetime of Nuclear Medium
Dt 3-5 fm/c resonances
t 10 fm/c 2 particle correlation
Partonic phase ?? 5-7 fm/c
30
Regeneration Cross Sections
Production channel for measured resonances
UrQMD calculations
Sp ? L(1520) Kp ? K NK? L(1520) Lp ? S(1385)
Regeneration/Rescattering cross section s(Sp)
lt s (Kp) lt s (Lp) ? L K
S
UrQMD predictions are in agreement with data.
Sascha Vogel, San Diego Winter Workshop 2006
hep-ph/0607242
31
No Medium in dAu Collissions
Phys. Rev. Lett. 97 (2006) 132301 e-Print
Archive nucl-ex/0604019
Resonances from late decay
32
Resonance Summary so far
Strong interacting hadronic medium after
chemical freeze-out (hadronization). ?
Thermal models do not describe all resonance
yields. ? Rescattering and regeneration of
resonances (ranking). ? Regeneration probes
hadronic interaction cross section of
strange baryons. ? Life-time between
freeze-outs 3-5 fm/c ?Partonic
life-time 5-7 fm/c ? Medium in dAu
?