Potential Energy - PowerPoint PPT Presentation
1 / 10
Title:
Potential Energy
Description:
Conservative force: ... For conservative forces W does not depend on the path chosen, only on the points ... work done by a conservative force on a particle ... – PowerPoint PPT presentation
Number of Views:41
Avg rating:3.0/5.0
Title: Potential Energy
1
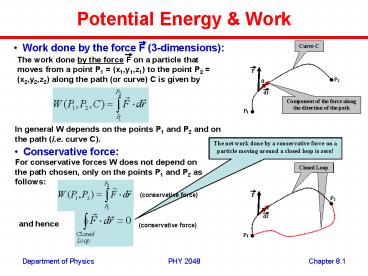
Potential Energy Work
- Work done by the force F (3-dimensions)
The work done by the force F on a particle that
moves from a point P1 (x1,y1,z1) to the point
P2 (x2,y2,z2) along the path (or curve) C is
given by
In general W depends on the points P1 and P2 and
on the path (i.e. curve C).
The net work done by a conservative force on a
particle moving around a closed loop is zero!
- Conservative force
For conservative forces W does not depend on the
path chosen, only on the points P1 and P2 as
follows
(conservative force)
and hence
(conservative force)
2
Potential Energy Work
- Potential Energy (3-dimensions)
The change in the potential energy in going from
the point P1 (x1,y1,z1) to the point P2
(x2,y2,z2) is defined to be the work done against
the conservative force F in going from P1 to P2.
Note that it is only the change in potential
energy, DU, that is well defined. The value of U
at one point (i.e. U(P1)) has no meaning and we
can choose it to be whatever we want.
Also, the potential energy can only be defined
for conservative forces since
(conservative force)
3
Potential Energy Examples
- Gravitational Potential Energy
Near the surface of the Earth the force of
gravity on a particle of mass m is
and
(gravitational potential energy)
Define U(0) 0 as the reference point!
- Elastic Potential Energy
For a (Hookes Law) block-spring system with
spring constant k the force on the block is
and
(elastic potential energy)
Define U(0) 0 as the reference point!
Note both gravity and the Hookes Law spring
(with no friction) are conservative forces!
4
Conservation of Mechanical Energy
- Mechanical Energy
The mechanical energy is defined to be the sum of
the kinetic energy, KE, and the potential energy,
U, as follows
For conservative forces, W DKE and DU -W.
Hence,
- Conservation of Mechanical Energy EMEC(P2)
EMEC(P1)
(isolated and conservative forces)
For an isolated system where only conservative
forces cause energy changes, the kinetic energy
and the potential energy can change, but their
sum, the mechanical energy Emec of the system
cannot change!
5
Conservation of Energy Examples
- Example (gravity)
A ball with mass M is released from rest a height
h above the surface of the Earth. What is its
speed when it reaches the surface (neglect air
resistance)?
- Example (gravity elastic spring)
A stone of mass M rests on an elastic spring
which is compressed a distance d0 by the stone.
The stone is pushed down an additional distance d
and then released. What is the maximum height,
H, reached by the stone relative to the release
point (i.e. y 0)? At what point, ymax, is the
kinetic energy of the stone the largest (i.e.
maximum speed)? (express the answers in terms of
d0 and d)
6
Conservation of Energy Examples
- Example (gravity elastic spring)
An elastic (Hookes Law) spring has an
unstretched length L. When a stone of mass M is
hung at rest from the spring, the spring is
stretched a distance d0. If the same stone is
now released from rest when the spring is
unstretched, what is the maximum distance d that
the spring is stretched? What is the maximal
kinetic energy of the store and how far is the
spring stretched when the stone has its maximal
kinetic energy? (express the answers in terms of
M, g, and d0)
(occurs at d0)
- Example (gravity)
A mass m is released from rest a height h above
the bottom of a circular loop-the-loop with
radius R. If the track is frictionless, what is
the minimum height such that the mass will make
it around the top of the circle without loosing
contact with the track?
7
Determining the Force from U
- Calculating the force F from the Potential Energy
(3-dimensions)
The potential is determined from the conservative
force F as follows
This means that
- Calculating the force F from the Potential Energy
(1-dimension)
The force in the x-direction is minus the slope
of U(x)
- Kinetic Energy
Classical turning point!
The region where U gt E is the classical forbidden
region!
8
Work Done by an External Force
Work is energy transferred to or from a system by
means of an external force acting on it.
- Case 1 (No Friction)
If there is no friction then the work done by an
external force goes into changing the total
mechanical energy as follows
(work done on system, no friction)
- Case 2 (with Friction)
If friction is present then some work done by the
external force goes into thermal energy ETH (i.e.
heating up the system) and
(work done on system, no friction)
- Increase in Thermal Energy DETH by Sliding
Suppose that a constant external force Fext pulls
a block with mass M to the right along the x-axis
and at t 0 the velocity of the block is v0 and
at a later time t after moving a distance d the
velocity of the block is v.
9
Conservation of Energy
- Total Energy
The total energy of a system is the sum of the
mechanical energy, EMEC, the thermal energy, ETH,
and the internal energy (in addition to thermal
energy), EINT
For an isolated system the total energy ETOT
cannot change!
The work done on a system by an external force
changes the total energy as follows
- Power
The power is the rate at which work by a force.
The power is also the rate at which energy is
transferred from one type to another
10
Conservation of Energy Examples
- Example (friction)
A block of mass M and initial velocity v0 is
sliding along the (negative) x-axis. The surface
is frictionless for x lt 0 and has a kinetic
coefficient of friction mk for x 0. At what
point x does the block come to a stop? (express
the answers in terms of v0, M, g, and mk)
- Example (friction and gravity)
A block of mass M and initial velocity v0 is
sliding along the (negative) x-axis. The surface
is frictionless for x lt 0 and has a kinetic
coefficient of friction mk for x 0. If the
block incounters an incline with angle q at x
0, at what point d along the incline does the
block come to a stop? (express the answers in
terms of v0, M, g, mk, and q)