Fundamentals of Audio Signals

1
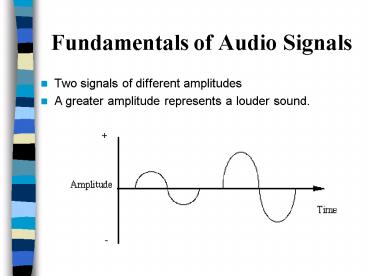
Fundamentals of Audio Signals

• Two signals of different amplitudes
• A greater amplitude represents a louder sound.

2
Fundamentals of Audio Signals

• Two signals of different frequencies
• A greater frequency represents a higher pitched
  sound.

3
Fundamentals of Audio Signals

• Any sound, no matter how complex, can be
  represented by a waveform.
• For complex sounds, the waveform is built up by
  the superposition of less complex waveforms
• The component waveforms can be discovered by
  applying the Fourier Transform
• Converts the signal to the frequency domain
• Inverse Fourier Transform converts back to the
  time domain

4
Sampling

• Sounds can be thought of as functions of a single
  variable (t) which must be sampled and quantized
• The sampling rate is given in terms of samples
  per second, or, kHz
• During the sampling process, an analog signal is
  sampled at discrete intervals
• At each interval, the signal is momentarily
  held and represents a measurable voltage rate

5
Quantization

• Audio is usually quantized at between 8 and 20
  bits
• Voice data is usually quantized at 8 bits
• Professional audio uses 16 bits
• Digital signal processors will often use a 24 or
  32 bit structure internally

6
Quantization

• The accuracy of the digital encoding can be
  approximated by considering the word length per
  sample
• This accuracy is known as the signal-to-error
  ratio (S/E) and is given by
• S/E 6n 1.8 dB
• n is the number of bits per sample

7
Quantization

• When a coarse quantization is used, it may be
  useful to add a high-frequency signal (analog
  white noise) to the signal before it is quantized
• This will make the coarse quantization less
  perceptible when the signal is played back
• This technique is known as dithering
• During the sampling process, an analog signal is
  sampled at discrete intervals
• At each interval, the signal is momentarily
  held and represents a measurable voltage rate

8
Channels

• We may also have audio data coming from more than
  one channels
• Data from a multichannel source is usually
  interleaved
• Sampling rates are always measured per channel
• Stereo data recorded at 8000 samples/second will
  actually generate 16,000 samples every second

9
Digital Audio Data

• A complete description of digital audio data
  includes (at least)
• sampling rate
• number of bits per sample
• number of channels (1 for mono, 2 for stereo,
  etc.)

10
Analog to Digital Conversion

• Nyquists theorem states that if an arbitrary
  signal has been run through a low-pass filter of
  bandwidth H, the filtered signal can be
  completely reconstructed by making only 2H
  (exact) samples per second.
• So, a low-pass filter is placed before the
  sampling circuitry of the analog-to-digital (A/D)
  converter.

11
Analog to Digital Conversion

• If frequencies greater than the Nyquist limit
  enter the digitization process, an unwanted
  condition called aliasing occurs
• The low-pass filter used will require the use of
  a gradual high-frequency roll-off, thus a
  sampling rate somewhat higher than twice the
  Nyquist limit is often used
• A/D conversion may make use of a successive
  approximation register (SAR)

12
Analog to Digital Conversion

• The low-pass filter can cause side effects.
• One way that these side effects can be overcome
  is through the use of oversampling - a
  signal-processing function that raises the sample
  rate of a digitally encoded signal.
• Consumer and professional 16-bit D/A converters
  often use up to 8- and 12-times oversampling,
  raising the sampling rate of a CD (for example)
  from 44.1 kHz to 352.8 kHz or 529.2 kHz.
• By altering the signals noise characteristics,
  it is possible to shift much of the overall
  bandwidth noise out of the range of human hearing.

13
Pulse Code Modulation

• The method that has been discussed for storing
  audio is known as pulse code modulation (PCM).

14
Pulse Code Modulation

• PCM is common in long-distance telephone lines.
• The analog signal (voice) is sampled at 8000
  samples/second with 7 or 8 bits per sample
• A T1 carrier handles 24 voice channels
  multiplexed together
• The bandwidth of this type of carrier can be
  calculated as follows
• 8 bits x 8000 samples/second x 24 channels
  1.544 Mbps
• Note that one out of 8 bits is for control, not
  data.

15
Pulse Code Modulation

• D/A conversion process
• parallelize the serial bit stream
• generate an analog voltage analogous to the
  voltage level at the original time of sampling
• An output sample and hold circuit is used to
  minimize spurious signal glitches
• a final low-pass filter is inserted into the path
• Smooths out the non-linear steps introduced by
  digital sampling

16
Pulse Code Modulation

• Other PCM topics
• mu-law and A-law companding
• DPCM
• DM
• ADPCM

17
Digital Signal Processing

• Processing of a digital signal to achieve special
  effects may generally be described in terms of
  some simple functions
• Addition
• Multiplication
• Delay
• Resampling

18
Digital Signal Processing

• Addition of two signals is accomplished by adding
  the sample values of the signals at each sampling
  point h(t)f(t)g(t)
• We can add as many signals as desired together
• Multiplication of a given signal is represented
  as g(t)mf(t), where m is the multiplication
  factor.
• Multiplication is used to increase or decrease
  the gain (loudness) of a signal. If m1, g is
  louder than f. If m
• Note that when adding signals together or
  multiplying by a number greater than one, care
  must be taken when the signal reaches the upper
  limit of the sample size

19
Digital Signal Processing

• Delay is an important effect described as
  follows g(t)f(td), where d is a delay time
• Use delay and addition to model echo
• f(t) HELLO
• g(t) f(t d1) , where 0
• g(t) HELLO
• h(t) f(t d2) , where 0
• h(t) HELLO
• F(t) f(t) g(t) h(t)
• HELLO HELLO HELLO

20
Digital Signal Processing

• Now consider a more realistic echo effect. We
  need to make each succeeding echo softer. We can
  do this with multiplication.
• g(t) mg(t) h(t) nh(t), 0
• F(t) f(t) g(t) h(t)
• HELLO HELLO HELLO

21
Digital Signal Processing

• When delays of 35-40 ms and greater are used, the
  listener perceives them as discrete delays
• Reducing the delay to the 15-35 ms range will
  create delays that are too closely spaced to be
  perceived as discrete delays
• When used with instruments, the brain is fooled
  into thinking that more instruments are playing
  than there actually are
• combining several short term delay modules that
  are slightly detuned in time, an effect known as
  chorusing can be achieved (used by guitarists,
  e.g.)

22
Pitch-Related Effects

• DSP functions are available that can alter the
  speed and pitch of an audio program. These can
• Change pitch without changing duration
• Change duration without changing pitch
• Change both duration and pitch
• The process for raising and lowering the pitch of
  a sample is shown on the next slides

23
Pitch-Related Effects
24
Pitch-Related Effects
25
Noise Elimination

• The noise elimination process can be seen to
  consist of three steps
• Visual analysis
• De-clicking
• De-noising
• Use visual analysis to determine the type of
  noise and to guide the next two steps

26
Noise Elimination

• De-clicking involves the removal of noise
  generated by analog side effects such as tape
  hiss, needle ticks, pops, etc.
• This is similar to snow removal in image
  processing
• (the noise manifests itself as large
  discontinuities in the sample waveform)
• The noise is likely to have affected more sample
  data in the audio file than in the corresponding
  image file
• A needle skip which affects 1/4 second of the
  file affects 11000 samples at the audio CD
  sampling rate
• Therefore, reconstruction of the affected area is
  not the straightforward linear interpolation
  process used in images
• Must examine a large portion of the waveform to
  reconstruct

27
Noise Elimination

• De-noising involves the removal of background
  noise such as hum, buzzes, air-conditioner
  noises, etc
• The waveform is analyzed to determine if louder
  sounds will mask the softer sound
• This involves breaking down the audio spectrum
  into a large number of frequency bands
• The signal is compared with a signature which
  represents the background noise. This is taken
  from a silent moment in the samplefile. It must
  be determined which portion of a signal is noise
  and whether the noise can be deleted without
  distorting the program

28
Digital Signal Processing

• Other DSP functions include digital mixing and
  sample rate conversion
• Digital mixing is the integration of a number of
  digital audio signals into a single ouput signal
• Sample rate conversion is necessary when a signal
  sampled at one rate must be played back on or
  transferred to equipment which uses another rate
• An example is the use of digital audio as the
  sound track for video. The incoming rate of 44.1
  kHz must be pulled-down to 44.056 kHz

29
Fading

• Fading is another important DSP function
• During a fade, the calculated sample amplitudes
  are either proportionately reduced or
  proportionately increased in level, according to
  a defined curve ramp
• For example, usually when performing a fade out,
  the signal will begin at a level that is 100
  percent of its current value and will reduce over
  the defined time to 0 percent
• Examples of various fade curves are shown in the
  following slides

30
Fading
31
Fading
32
Fading

• To find the linearly faded value of a sample at
  time tx, t0txt1, we use the following equation
• s(tx) s(tx) (tx - t0) / (t1 - t0)
• We can also combine the fade in of one soundfile
  with the fade out of another soundfile to produce
  the effect known as crossfade

33
Fading
34
Fading

• Note that the two curves intersect at 50
  attenuation and that the sum of the two values at
  any point in time is always 100
• Thus, we can add together the two signals to form
  our crossfaded signal and the amplitude of the
  waveform will never be greater than the maximum
  possible amplitude