Circle Scan Conversion

1
Circle Scan Conversion
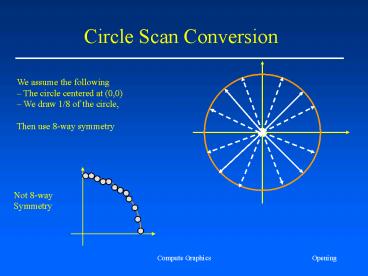
We assume the following The circle centered at
(0,0) We draw 1/8 of the circle, Then use
8-way symmetry
Not 8-way Symmetry
2
Circle Scan Conversion

• We assume (xp, yp) has been correctly
• Selected.
• The slope is between 0 and 1.0
• If the circle passes above M, then
• We select E
• Else
• We select SE

E
M
ME
SE
MSE
We assume The circle centered at (0,0) We
draw 1/8 of the circle, Then use 8-way symmetry
3
Circle Scan Conversion

• We use D as in the case of line
• D F(M) F(xp1, yp-0.5)
• (xp1)2(yp-0.5)2-R2
• If ( D lt 0 ) then
• M is below the arc,
• pixel E is closer to the line.
• If (D gt 0 ) then
• M is above the arc,
• pixel SE is closer to the line.

4
Circle Scan Conversion

• CASE I E is next
• We use D as in the case of line
• Dnew F(ME) F(xp2, yp-0.5)
• (xp2)2(yp-0.5)2-R2
• D ( 2xp3)
• CASE II SE is next
• We use D as in the case of line
• Dnew F(M) F(xp2, yp-1.5)
• (xp2)2(yp-1.5)2-R2
• D ( 2xp-2yp5)
• Initialization
• DinitF(1,R-0.5)

5
Circle Scan Conversion
DrawCircel(int radius, Color clr) int x 0
int y radius int d 1-radius
Plot(x,y, clr) while ( y gt x ) if
( d lt 0 ) // E Selected d 2x 3
else d 2(x-y) 5
y-- x
Plot(x,y, clr)
6
Circle Scan Conversion

• Let us use second order difference
• If E was selected then
• ?Eold 2xp3
• ?Enew 2(xp1)3
• deltaE ?Enew - ?Eold 2
• If SE was selected then
• ?SEold 2xp-2yp5
• ?SEnew 2(xp1)-2yp 5
• deltaSE ?SEnew - ?SEold 4

E
M
ME
SE
MSE
7
Circle Scan Conversion
DrawCircel(int radius, Color clr) int x 0
, y radius int d 1-radius int
deltaE 3, deltaSE -2radius 5
Plot(x,y, clr) while ( y gt x ) if (
d lt 0 ) // E Selected d deltaE
deltaE 2 deltaSE 2
else // SE Selected d
deltaSE deltaE 2 deltaSE
4 y-- x
Plot(x,y, clr)