FIBONACCI

1
(No Transcript)
2
Biography (1170-1250)

• Fibonacci is a short for the Latin "filius
  Bonacci" which means
• "the son of Bonacci" but his full name was
  Leonardo of Pisa, or
• Leonardo Pisano in Italian since he was born in
  Pisa (Italy).
• He was educated in North Africa where his father
  worked as a merchant.
• Fibonacci travelled widely with his father
  around the Mediterranean coast .
• In 1200 he returned to Pisa and used the
  knowledge he had gained on his travels to write
  his books.

3
Books

• Liber Abaci (1202), The Book of Calculation
• Practica Geometriae (1220), The Practice of
  Geometry
• Flos (1225), The Flower
• Liber Quadratorum (1225),The Book of Square
  Numbers

4
The Flower

• the approximate solution of the following cubic
  equation
• x³2x²10x20
• in sexagesimal notation is 1.22.7.42.33.4.40 ,
  equivalent to

5
The Book of Square Numbers

• Method to find Pythogorean triples
• When you wish to find two square numbers
  whose addition produces a square number, you take
  any odd square number as one of the two square
  numbers and you find the other square number by
  the addition of all the odd numbers from unity up
  to but excluding the odd square number. For
  example, you take 9 as one of the two squares
  mentioned the remaining square will be obtained
  by the addition of all the odd numbers below 9,
  namely 1, 3, 5, 7, whose sum is 16, a square
  number, which when added to 9 gives 25, a square
  number.

6
Liber Abaci

• The book introduced the Hindu-Arabic number
  system into Europe , the system we use today,
  based on ten digits with its decimal point and a
  symbol for zero
• 1 2 3 4 5 6 7 8 9 0
• The book describes (in Latin) the rules for
  adding numbers, subtracting, multiplying and
  dividing.

7
Rabbits

• Suppose a newly-born pair of rabbits ( male
  female) are put in a field. Rabbits are able to
  mate at the age of one month so that at the end
  of its second month a female can produce another
  pair of rabbits. Suppose that our rabbits never
  die and that the female always produces one new
  pair ( male female) every month from the second
  month on.
• How many pairs will
• there be in one year?!

8
Answer

• At the end of the first month, they mate, but
  there is still only 1 pair
• At the end of the second month the female
  produces a new pair, so now there are 2 pairs of
  rabbits in the field.
• At the end of the third month, the original
  female produces a second pair, making 3 pairs in
  all in the field.
• At the end of the fourth month, the original
  female has produced yet another new pair, the
  female born two months ago produces her first
  pair also, making 5 pairs..

9
(No Transcript)
10
We get the following sequence of numbers 1, 1,
2, 3, 5, 8, 13, 21, 34 ...

• This sequence, in which each number is a sum of
  two previous is called Fibonacci sequence so
  there is the simple rule add the last two to get
  the next!
•  
• The Fibonacci numbers are the sequence of numbers
  defined by the linear recurrence equation
• F(n)F(n-1)F(n-2)

11
Fibonacci Rectangles

• We start with two small squares of size 1 next to
  each other. On top of both of these we draw a
  square of size 2 (11). We can now draw a new
  square - touching both a unit square and the
  latest square of side 2 - so having sides 3 units
  long and then another touching both the 2-square
  and the 3-square (which has sides of 5 units). We
  can continue adding squares around the picture,
  each new square having a side which is as long as
  the sum of the latest two square's sides. This
  set of rectangles whose sides are two successive
  Fibonacci numbers in length and which are
  composed of squares with sides which are
  Fibonacci numbers, we call the Fibonacci
  Rectangles.

12
Rectangles
13

• Fibonacci spirals
• A spiral drawn in the squares, a quarter of a
  circle in each square.

14
PASCALS TRIANGLE
15
Nature

• One of the most fascinating things about the
  Fibonacci numbers is their connection to nature.
• the number of petals, leaves and branches
• spiral patterns in shells
• spirals of the sunflower head
• pineapple scales

16
Flowers
17
(No Transcript)
18
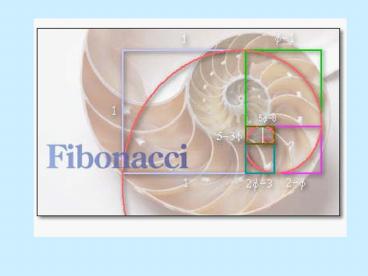
Nautilus
19
Sun

• Flower

20
Pineapple
21
Conclusion

• The greatest European mathematician of the middle
  age, most famous for the Fibonacci sequence, in
  which each number is the sum of the previous two
  and for his role
• in the introduction to Europe
• of the modern
• Arabic decimal system.

22
HAPPY EASTER!!!
23
THE ENDBYE