Non-Ideal VLE Calculations

1
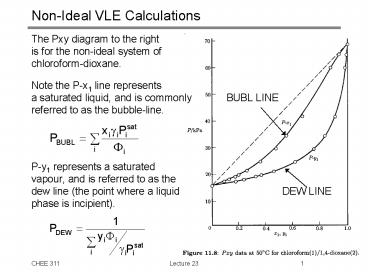
Non-Ideal VLE Calculations

• The Pxy diagram to the right
• is for the non-ideal system of
• chloroform-dioxane.
• Note the P-x1 line represents
• a saturated liquid, and is commonly BUBL LINE
• referred to as the bubble-line.
• P-y1 represents a saturated
• vapour, and is referred to as the
• dew line (the point where a liquid DEW
  LINE
• phase is incipient).

2
Non-Ideal BUBL P Calculations

• The simplest VLE calculation of the five is the
  bubble-point pressure calculation.
• Given T, x1, x2,, xn Calculate P, y1, y2,,
  yn
• To find P, we start with a material balance on
  the vapour phase
• Our equilibrium relationship provides
• (14.8)
• which yields the Bubble Line equation when
  substituted into the material balance
• or
• (14.10)

3
Non-Ideal BUBL P Calculations

• Non-ideal BUBL P calculations are complicated by
  the dependence of our coefficients on pressure
  and composition.
• Given T, x1, x2,, xn Calculate P, y1, y2,,
  yn
• To apply the Bubble Line Equation
• requires
• ?
• ?
• ?
• Therefore, the procedure is
• calculate Pisat, and ?i from the information
  provided
• assume ?i1, calculate an approximate PBUBL
• use this estimate to calculate an approximate ?i
• repeat PBUBL and ?i calculations until solution
  converges.

4
Non-Ideal Dew P Calculations

• The dew point pressure of a vapour is that
  pressure which the mixture generates an
  infinitesimal amount of liquid. The basic
  calculation is
• Given T, y1, y2,, yn Calculate P, x1, x2,, xn
  
• To solve for P, we use a material balance on the
  liquid phase
• Our equilibrium relationship provides
• (14.9)
• From which the Dew Line expression needed to
  calculate P is generated
• (14.11)

5
Non-Ideal Dew P Calculations

• In trying to solve this equation, we encounter
  difficulties in estimating thermodynamic
  parameters.
• Given T, y1, y2,, yn Calculate P, x1, x2,, xn
• ?
• ?
• ?
• While the vapour pressures can be calculated, the
  unknown pressure is required to calculate ?i, and
  the liquid composition is needed to determine ?i
• Assume both parameters equal one as a first
  estimate, calculate P and xi
• Using these estimates, calculate ?i
• Refine the estimate of xi and estimate ?i
  ((12.10ab)
• Refine the estimate of P
• Iterate until pressure and composition converges.

6
8. Non-Ideal Bubble and Dew T Calculations

• The Txy diagram to the right
• is for the non-ideal system of
• ethanol(1)/toluene(2) at P 1atm.
• Note the T-x1 line represents
• a saturated liquid, and is commonly DEW
  LINE
• referred to as the bubble-line.
• T-y1 represents a saturated
• vapour, and is referred to as the
• dew line (the point where a liquid
• phase is incipient).
• BUBL LINE

7
Non-Ideal BUBL T Calculations

• Bubble point temperature calculations are among
  the more complicated VLE problems
• Given P, x1, x2,, xn Calculate T, y1, y2,,
  yn
• To solve problems of this sort, we use the Bubble
  Line equation
• 14.10
• The difficulty in determining non-ideal bubble
  temperatures is in calculating the thermodynamic
  properties Pisat, ?i, and ?i.
• Since we have no knowledge of the temperature,
  none of these properties can be determined before
  seeking an iterative solution.

8
Non-Ideal BUBL T Calculations Procedure

• 1. Estimate the BUBL T
• Use Antoines equation to calculate the
  saturation temperature (Tisat) for each component
  at the given pressure
• Use TBUBL ? xi Tisat as a starting point
• 2. Using this estimated temperature and xis
  calculate
• Pisat from Antoines equation
• Activity coefficients from an Excess Gibbs Energy
  Model (Margules, Wilsons, NRTL)
• Note that these values are approximate, as we are
  using a crude temperature estimate.

9
Non-Ideal BUBL T Calculations Procedure

• 3. Estimate ?i for each component.
• We now have estimates of T, Pisat and ?i, but no
  knowledge of ?i.
• Assume that ?i1 and calculate yis using
• 14.8
• Plug P, T, and the estimates of yis into your
  fugacity coefficient expression to estimate ?i.
• Substitute these?i estimates into 12.9 to
  recalculate yi and continue this procedure until
  the problem converges.
• Step 3 provides an estimate of ?i that is based
  on the best T, Pisat, ?i, and xi data that is
  available at this stage of the calculation.
• If you assume that the vapour phase is a perfect
  gas mixture, all ?i 1.

10
Non-Ideal BUBL T Calculations Procedure

• 4. Our goal is to find the temperature that
  satisfies our bubble point equation
• (14.10)
• Our estimates of T, Pisat, ?i and ?i, are
  approximate since they are based on a crude
  temperature estimate (T ? xi Tisat)
• Calculate P using the Bubble Line equation
  (12.11)
• If Pcalc lt Pgiven then increase T
• If Pcalc gt Pgiven then decrease T
• If Pcalc Pgiven then T TBUBL
• The simplest method of finding TBUBL is a trial
  and error method using a spreadsheet.
• Follow steps 1 to 4 to find Pcalc.
• Change T and repeat steps 2, 3, and 4 until Pcalc
  Pgiven

11
Non-Ideal DEW T Calculations

• The dew point temperature of a vapour is that
  which generates an infinitesimal amount of
  liquid.
• Given P, y1, y2,, yn Calculate T, x1, x2,, xn
  
• To solve these problems, use the Dew Line
  equation
• 14.11
• Once again, we havent sufficient information to
  calculate the required thermodynamic parameters.
• Without T and xis, we cannot determine ?i, ?i
  or Pisat.

12
Non-Ideal DEW T Calculations Procedure

• 1. Estimate the DEW T
• Using P, calculate Tisat from Antoines equation
• Calculate T ? yi Tisat as a starting point
• 2. Using this temperature estimate and yis,
  calculate
• Pisat from Antoines equation
• ?i using the virial equation of state
• Note that these values are approximate, as we are
  using a crude temperature estimate.

13
Non-Ideal DEW T Calculations Procedure

• 3. Estimate ?i, for each component
• Without liquid composition data, you cannot
  calculate activity coefficients using excess
  Gibbs energy models.
• A. Set ?i1
• B. Calculate the Dew Pressure
• C. Calculate xi estimates from the equilibrium
  relationship
• D. Plug P,T, and these xis into your activity
  coefficient model to estimate ?i for each
  component.
• E. Substitute these ?i estimates back into 12.12
  and repeat B through D until the problem
  converges.

14
Non-Ideal DEW T Calculations Procedure

• 4. Our goal is to find the temperature that
  satisfies our Dew Line equation
• (14.11)
• Our estimates of T, Pisat, ?i and ?i, are based
  on an approximate temperature (T ? xi Tisat) we
  know is incorrect.
• Calculate P using the Bubble Line equation
  (14.10)
• If Pcalc lt Pgiven then increase T
• If Pcalc gt Pgiven then decrease T
• If Pcalc Pgiven then T TDew
• The simplest method of finding TDew is a trial
  and error method using a spreadsheet.
• Follow steps 1 to 4 to find Pcalc.
• Change T and repeat steps 2, 3, and 4 until Pcalc
  Pgiven

15
9.3 Modified Raoults Law

• At low to moderate pressures, the vapour-liquid
  equilibrium equation can be simplified
  considerably.
• Consider the vapour phase coefficient, ?i
• Taking the Poynting factor as one, this quantity
  is the ratio of two vapour phase properties
• Fugacity coefficient of species i in the mixture
  at T, P
• Fugacity coefficient of pure species i at T,
  Pisat
• If we assume the vapour phase is a perfect gas
  mixture, this ratio reduces to one, and our
  equilibrium expression becomes,
• or

1
16
Modified Raoults Law

• Using this approximation of the non-ideal VLE
  equation simplifies phase equilibrium
  calculations significantly.
• Bubble Points
• Setting ?i 1makes BUBL P calculations very
  straightforward.
• Dew Points