8. VLE Flash Calculations for Non-Ideal Systems

1
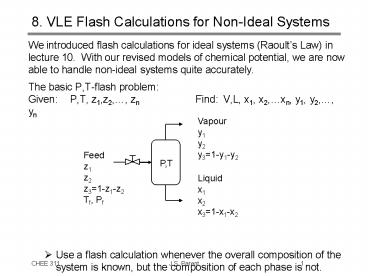
8. VLE Flash Calculations for Non-Ideal Systems

• We introduced flash calculations for ideal
  systems (Raoults Law) in lecture 10. With our
  revised models of chemical potential, we are now
  able to handle non-ideal systems quite
  accurately.
• The basic P,T-flash problem
• Given P,T, z1,z2,, zn Find V,L, x1,
  x2,xn, y1, y2,, yn
• Use a flash calculation whenever the overall
  composition of the system is known, but the
  composition of each phase is not.

2
VLE Flash Calculations from a Phase Diagram

• To the right is the Txy diagram for the
• highly non-ideal system of Ethanol(1)-
• Toluene(2) at P1 atm.
• 1. Given a feed stream containing 25
• ethanol, between what temperatures
• do we have two phases?
• 2. At 90C, what are the compositions
• of the liquid and vapour streams?
• 3. Under these conditions, what fraction
• of the system exists as a vapour?

3
VLE Flash Equation

• When a phase diagram is not at hand, a flash
  calculation using a model for the phase behaviour
  is required.
• Whenever confronted with a flash problem, apply
  one of the general flash equations
• 12.27
• or
• 12.28
• This is the most versatile approach to solving
  flash problems
• In all but simple P,T flashes for binary systems,
  the general flash equation will produce the
  quickest answer.

4
Partition Coefficient, Ki

• The partition coefficient, Ki yi / xi, is used
  to simplify the general flash equation.
• It reflects the tendency of a component to
  vapourize. Those components with a large
  partition coefficient (Ki gt1) concentrate in the
  vapour, while those with Ki lt1 concentrate in the
  liquid phase.
• The partition coefficient in a VLE system is
  provided by our phase equilibrium expression
  (derived from equivalence of chemical potential).
  Recall,
• Therefore,
• Note that for a non-ideal system, Ki is a
  function of P,T and the compositions of both the
  liquid and vapour phase.

5
Solving Non-Ideal Flash Problems

• The Classic P,T-flash problems involves
• Given P,T, z1,z2,, zn Find V,L, x1, x2,xn,
  y1, y2,, yn
• For a three component system, the VLE flash
  equation is
• 12.28
• Or, substituting for the partition coefficients
• The general solution involves
• Find the vapour phase fraction (V?0) that
  satisfies 12.28.
• Substitute V into
• and solve for yi using

6
Solving Non-Ideal Flash Problems

• The non-ideal flash equation requires knowledge
  of the vapour and liquid compositions to evaluate
  ?i and ?i, respectively.
• These are the unknowns that we are attempting to
  calculate
• Therefore, flash calculations always require
  iteration.
• Suppose you are given P,T, z1, z2, z3 and you are
  asked to find V, and the phase compositions.
• 1. Calculate the DEWP and BUBLP of the feed at
  the given temperature to ensure that two phases
  exist.
• 2. Use Raoults law to simplify the flash problem
  to the degree that it can (easily?) be solved.
• This involves setting ?i 1 and Fi 1 for all
  components
• Calculate Pisat for each component at the given T
• Solve for V using the flash equation, 12.28
• Solve for xi, and yi
• These are ESTIMATES that serve only to get us
  started!

7
Solving Non-Ideal Flash Problems

• 3. Using the latest estimate of xi and yi, along
  with the P,T given, calculate
• ?i for each component using an activity
  coefficient model
• Fi for each component using an equation of state
  for the vapour.
• Calculate Ki ?iPisat / FiP for each component
• 4. Using the revised partition coefficients,
  calculate V through a trial and error procedure
  on the general flash calculation.
• 5. Recalculate xi,and yi for each component.
• 6. Repeat steps 3 through 5 until the solution
  converges.

8
8. Azeotropic Mixtures SVNA 12.3,12.5

• Large deviations from ideal liquid solution
  behaviour relative to the difference between the
  pure component vapour pressures result in
  azeotrope formation.
• In CHEE 311, we are interested in
• 1. Describing azeotropic mixtures both physically
  and in thermodynamic terms.
• 2. Detecting azeotropic conditions and
  calculating their composition.

9
Azeotropic Mixtures
Water / Hydrazine, P1atm Water / Pyridine,
P1atm
10
Azeotropes - Impact on Separation Processes

• Separation processes that exploit
• VLE behaviour (flash operations,
• distillation) are influenced greatly
• by azeotropic behaviour.
• An azeotropic mixture boils
• to evolve a vapour of the
• same composition and,
• conversely,condenses to
• generate a liquid of the
• same composition.
• Ethanol(1)/Toluene(2) at P1 atm

11
Predicting Whether an Azeotrope Exists

• To determine whether an azeotrope will be
  encountered at a given pressure and temperature,
  we define the relative volatility. For a binary
  system, a12 is
• 12.21
• where xi and yi are the mole fractions of
  component i in the liquid and vapour fractions,
  respectively.
• At an azeotrope, the composition of the vapour
  and liquid are identical. Since, y1x1 and y2x2
  at this condition,
• To determine whether an azeotropic mixture
  exists, we need to determine whether at some
  composition, a12 can equal 1.

12
Predicting Whether an Azeotrope Exists

• We can derive an expression for a12 using
  modified Raoults Law as our phase equilibrium
  relationship,
• which when substituted into the relative
  volatility, yields
• 12.22
• a12 is therefore a function of T (Pisat, gi) and
  the composition of the liquid phase. Calculation
  of a12 therefore requires
• Antoines equation
• an activity coefficient model (Margules,
  Wilsons, )
• a liquid composition
• Our goal is to determine whether an azeotrope
  exists.
• At some composition, can a121?

13
Predicting Whether an Azeotrope Exists

• One means of determining whether a121 is
  possible is to evaluate the function (Eqn12.22)
  over the entire composition range.
• This is plotted for the ethanol(1)/toluene(2)
  system using Wilsons equation to describe liquid
  phase non-ideality.
• According to this plot, a121 at x1 0.82,
  meaning that an azeotrope exists at this
  composition.

14
Predicting Whether an Azeotrope Exists

• Because equation 12.22 is continuous and
  monotonic, we do not need to evaluate a12 over
  the whole range of x1.
• It is sufficient to calculate a12 at the
  endpoints, x10 and x11
• At x1 0, we have
• and at x1 1, we have
• If one of these limits has a value greater than
  one, and the other less than one, at some
  intermediate composition we know a12 1.
• This is a simple means of determining whether an
  azeotrope exists.

15
Determining the Composition of an Azeotrope

• For an azeotropic mixture, the relative
  volatility equals one
• at an azeotrope.
• To find the azeotropic composition, two methods
  are available
• trial and error (spreadsheet)
• analytical solution
• Rearranging 12.22 as above yields
• The azeotropic composition is that which
  satisfies this equation.
• Substitute an activity coefficient model for g1,
  and g2.
• Solve for x1.

16
8. Dilute Liquid Solution Approximations

• There are many non-ideal systems in which one
  component is significantly more volatile than
  others. In these cases, the liquid phase is very
  rich in the heavy components, and lean in the
  light component.
• The most common system encountered in
  environmental and biochemical engineering is H2O
  (1) / O2 (2).
• The very low O2 content found in the liquid phase
  under practical engineering conditions allows us
  to simplify phase equilibrium calculations
• for H2O
• for O2
• Since the origin of most non-ideal behaviour is
  found in the liquid, we will focus on
  simplifications to liquid phase properties.

17
Rigorous Treatment of Liquid Mixture Fugacity

• Shown is a plot of the mixture fugacities of MEK
  (1) and Toluene (2) at 50C as a function of
  liquid composition
• For component 1, MEK
• For component 2, Toluene

18
Dilute Liquid Solution Approximations

• Figure 11.3 of SVNA illustrates the fugacity of a
  component in a liquid mixture.
• Note that the Lewis-Randall rule applies for the
  predominate component of a liquid solution
• x1?1 ?1 ?1, f1l ? f1l x1
• If the component is present in very small amounts
  (x1 lt 0.02), its mixture fugacity can be
  approximated by a linear relationship, such that
• x1?0 f1l ? k1x1

19
Dilute Solution Simplifications Heavy Component

• For the heavy component (1) of a dilute solution,
  we can apply the Lewis-Randall rule
• The equilibrium relationship for the heavy
  component (such as H2O in the water-oxygen
  system) becomes
• or,
• or,
• for the predominate component in solution
  (x1gt0.98)

20
Dilute Solution Simplifications Light Component

• For the light component (2) of a dilute liquid
  solution, we create a new construct, the Henrys
  constant, k2
• (11.2)
• This is the slope of the f2l vs x2 curve as x2 ?
  0.
• The Henrys constant is tabulated for a specific
  system at a given temperature.
• The equilibrium relationship for the light
  component (such as O2 in the water-oxygen system)
  becomes
• where the Henrys constant, k2 is that of oxygen
  in water at the temperature of interest.

21
Dilute Liquid Solution Approximations Example 1

• Suppose we are designing a bioreactor in which
  pure O2 is bubbled through an aqueous medium to
  replenish the oxygen consumed by the cell
  culture.
• The process is operated at atmospheric pressure
  and a temperature of 25C.
• How do we define a thermodynamic system that
  provides relevant phase equilibrium data?
• What is the concentration of oxygen in the liquid
  phase, given a Henrys Coefficient, kO2 4400
  MPa at 25C?

22
Dilute Liquid Solution Approximations Example 2

• As a research engineer in a hydrogenation plant,
  you are asked to compile VLE data on the H2 /
  chlorobenzene system in a way that plant
  engineers can readily apply.
• The objective is to conduct VLE experiments on
  the system, treat the data according to
  thermodynamic theory, and summarize the results
  in a simple manner.
• How will you start?
• What simplifications can be made?
• In what form will you summarize the data?