Additive Rule/ Contingency Table

1
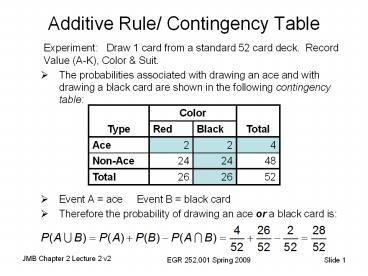
Additive Rule/ Contingency Table

• Experiment Draw 1 card from a standard 52
  card deck. Record Value (A-K), Color Suit.
• The probabilities associated with drawing an ace
  and with drawing a black card are shown in the
  following contingency table
• Event A ace Event B black card
• Therefore the probability of drawing an ace or a
  black card is

Type Color Color Total
Type Red Black Total
Ace 2 2 4
Non-Ace 24 24 48
Total 26 26 52
2
Short Circuit Example - Data

• An appliance manufacturer has learned of an
  increased incidence of short circuits and fires
  in a line of ranges sold over a 5 month period. A
  review of the defect data indicates the
  probabilities that if a short circuit occurs, it
  will be at any one of several locations is as
  follows
• The sum of the probabilities equals _____

Location P
House Junction (HJ) 0.46
Oven/MW junction (OM) 0.14
Thermostat (T) 0.09
Oven coil (OC) 0.24
Electronic controls (EC) 0.07
3
Short Circuit Example - Probabilities

• If we are told that the probabilities represent
  mutually exclusive events, we can calculate the
  following
• The probability that the short circuit does not
  occur at the house junction is
• P(HJ) 1 - P(HJ) 1 0.46 0.54
• The probability that the short circuit occurs at
  either the Oven/MW junction or the oven coil is
• P(OM U OC) P(OM)P(OC) 0.14 0.24 0.38

4
Conditional Probability

• The conditional probability of B given A is
  denoted by P(BA) and is calculated by
• P(BA) P(B n A) / P(A)
• Example
• S 1,2,3,4,5,6,7,8,9,11
• Event A number greater than 6 P(A) 4/10
• Event B odd number P(B) 6/10
• (BnA) 7, 9, 11 P (BnA) 3/10
• P(BA) P(B n A) / P(A) (3/10) / (4/10) 3/4

5
Multiplicative Rule

• If in an experiment the events A and B can both
  occur, then
• P(B n A) P(A) P(BA)
• Previous Example
• S 1,2,3,4,5,6,7,8,9,11
• Event A number greater than 6 P(A) 4/10
• Event B odd number P(B) 6/10
• P(BA) 3/4 (calculated in previous slide)
• P(BnA) P(A)P(BA) (4/10)(3/4) 3/10

6
Independence Definitions

• If in an experiment the conditional probabilities
  P(AB) and P(BA) exist, the events A and B are
  independent if and only if
• P(AB) P(A) or P(BA) P(B)
• Two events A and B are independent if and only if
  P A n B P(A) P(B)

7
Independence Example

• A quality engineer collected the following data
  on 100 defective items produced by a manufacturer
  in the southeast

Problem/Shift Electrical Mechanical Other
Day 20 15 25
Night 10 20 10

• What is the probability that the defective items
  were associated with the day shift?
• P(Day) (201525) / 100 .60 or 60
• What was the relative frequency of defectives
  categorized as electrical?
• (20 10) / 100 P(Electrical) .30
• Are Electrical and Day independent?
• P(E n D) 20 / 100 .20 P(D) P(E)
  (.60) (.30) .18
• Since .20 ?.18, Day and Electrical are not
  independent.

8
Serial and Parallel Systems

• For increased safety and reliability, systems are
  often designed with redundancies. A typical
  system might look like the following

If components are in serial (e.g., A B), all
must work in order for the system to work.
If components are in parallel, the system works
if any of the components work.
9
Serial and Parallel Systems
1

• What is the probability that
• Segment 1 works?
• A and B in series
• P(AnB) P(A) P(B) (0.95)(0.9) 0.855
• Segment 2 works?
• C and D in parallel will work unless both C and D
  do not function
• 1 P(C) P(D) 1 (0.12) (0.15)
  1-0.018 0.982
• The entire system works?
• Segment 1, Segment 2 and E in series
• P(Segment1) P(Segment2) P(E)
  0.8550.9820.97 0.814

2