Network Flow Problems

1
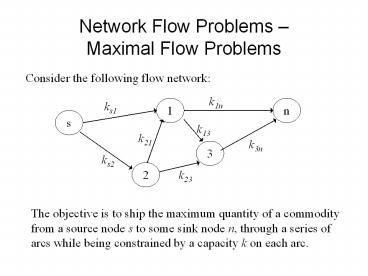
Network Flow Problems Maximal Flow Problems
Consider the following flow network
k1n
ks1
1
n
s
k13
k21
k3n
3
ks2
2
k23
 
The objective is to ship the maximum quantity of
a commodity from a source node s to some sink
node n, through a series of arcs while being
constrained by a capacity k on each arc.
2
Maximal Flow Problems

• Examples
• Maximize the flow through a companys
  distribution network from its factories to its
  customers.
• Maximize the flow through a companys supply
  network from its vendors to its factories.
• Maximize the flow of oil through a system of
  pipelines.
• Maximize the flow of water through a system of
  aqueducts.
• Maximize the flow of vehicles through a
  transportation network.

 
3
Maximal Flow Problems
Definitions Flow network consists of nodes and
arcs Source node node where flow
originates Sink node node where flow
terminate Transshipment points intermediate
nodes Arc/Link connects two nodes Directed arc
arc with direction of flow indicated Undirected
arc arc where flow can occur in either
direction Capacity(kij) maximum flow possible
for arc (i,j) Flow(f ij) flow in arc (i,j).
Forward arc arcs with flow out of some
node Backward arc arc with flow into some
node Path series of nodes and arcs between some
originating and some terminating node Cycle
path whose beginning and ending nodes are the same
 
4
Maximal Flow Problems LP Formulation
f
1
n
f
s
3
2
Objective Maximize Flow (f) Constraints 1) The
flow on each arc, fij, is less than or equal to
the capacity on each arc, kij. 2) Conservation
of flow at each node. Flow in flow out.
 
5
Maximal Flow Problems LP Formulation
f
1
n
f
s
3
Max Z f st s) fs1 fs2 f 1) f13 f1n
fs1 f21 2) f21 f23 fs2 3) f3n f13
f23 n) f f3n f1n 0 lt fij lt kij

2

• Objective Maximize Flow (f)
• Constraints
• The flow on each arc, fij, is less than or
• equal to the capacity on each arc, kij.
• Conservation of flow at each node.
• Flow in flow out.

 
6
Maximal Flow Problems Conversion to Standard
Form
What if there are multiple sources and/or
multiple sinks?
n1
s1
1
n2
 
3
s2
2
7
Maximal Flow Problems Conversion to Standard
Form
Create a supersource and supersink with arcs
from the supersource to the original sources and
from the original sinks to the supersink. What
capacity should we assign to these new arcs?
n1
f
s1
n
1
f
s
n2
 
 
3
s2
2
8
Maximal Flow Problems Conversion to Standard
Form
What if there is an undirected arc (flow can
occur in either direction)? See arc (1,2).
f
1
n
f
s
k12
3
 
2
9
Maximal Flow Problems Conversion to Standard
Form
Create two directed arcs with the same capacity.
Upon solving the problem and obtaining flows on
each arc, replace the two directed arcs with a
single arc with flow fij fji , in the
direction of the larger of the two flows.
f
1
n
f
s
k21
k12
3
 
2
10
Maximal Flow Problems Lingo Solution
11
Maximal Flow Problems Excel Solution