An Introduction to Limits

1
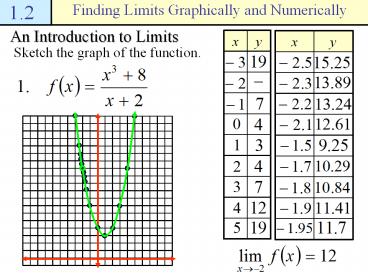
An Introduction to Limits
x y









x y









Sketch the graph of the function.
2
An Introduction to Limits
Definition of a limit
We say that the limit of f(x) is L as x
approaches a and write this as
provided we can make f(x) as close to L as we
want for all x sufficiently close to a, from both
sides, without actually letting x be a.
3
Estimating a limit numerically
Example 1
Estimate the value of the following limit.
x y








Limits are asking what the function is doing
around x a, and are not concerned with
what the function is actually doing at x a.
 
4
Finding a limit
Example 2
Estimate the value of the following limit.
 
5
Behavior that differs from the right and left
Example 3
Estimate the value of the following limit.
 
 
6
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
-5
-4
-3
0
1
2
3
4
5
6
Unbounded behavior
Example 4
Estimate the value of the following limit.
 
 
7
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Oscillating behavior
Example 5
Estimate the value of the following limit.
t f (t)








 
8
The Formal Definition of a Limit
Let f(x) be a function defined on an interval
that contains x a, except possibly at x a.
Then we say that,
 
if for every number e gt 0 there is some number d
gt 0 such that
whenever
9
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
Finding a d for a given e
Example 6
Given the limit
find d such that
whenever
 
10
(No Transcript)
11
Pg. 46, 1.1 1-11