Calculus 6.5

1
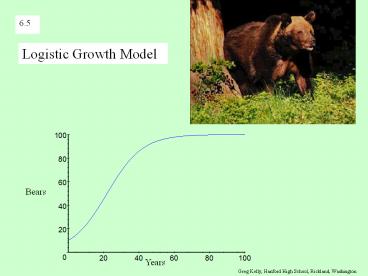
6.5
Logistic Growth Model
Bears
Years
Greg Kelly, Hanford High School, Richland,
Washington
2
The exponential growth equation occurs when the
rate of growth is proportional to the amount
present.
If we use P to represent the population, the
differential equation becomes
The constant k is called the relative growth rate.
3
However, real-life populations do not increase
forever. There is some limiting factor such as
food, living space or waste disposal.
There is a maximum population, or carrying
capacity, M.
4
The equation then becomes
Our book writes it this way
We can solve this differential equation to find
the logistics growth model.
5
Logistics Differential Equation
6
Logistics Differential Equation
7
Logistics Differential Equation
8
(No Transcript)
9
Example
Logistic Growth Model
Ten grizzly bears were introduced to a national
park 10 years ago. There are 23 bears in the
park at the present time. The park can support a
maximum of 100 bears.
Assuming a logistic growth model, when will the
bear population reach 50? 75? 100?
10
Ten grizzly bears were introduced to a national
park 10 years ago. There are 23 bears in the
park at the present time. The park can support a
maximum of 100 bears.
Assuming a logistic growth model, when will the
bear population reach 50? 75? 100?
11
At time zero, the population is 10.
12
After 10 years, the population is 23.
13
We can graph this equation and use trace to
find the solutions.
y50 at 22 years
y75 at 33 years
y100 at 75 years
p