Solve a simple absolute value equation - PowerPoint PPT Presentation
Title:
Solve a simple absolute value equation
Description:
Title: PowerPoint Presentation Author: administrator Last modified by: kimemach3- Created Date: 6/28/2006 5:09:04 AM Document presentation format – PowerPoint PPT presentation
Number of Views:132
Avg rating:3.0/5.0
Title: Solve a simple absolute value equation
1
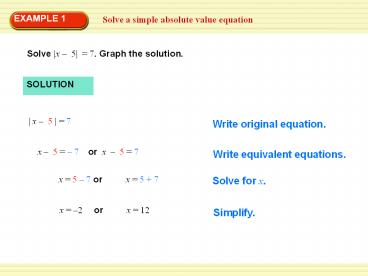
EXAMPLE 1
Solve a simple absolute value equation
Solve x 5 7. Graph the solution.
SOLUTION
x 5 7
Write original equation.
x 5 7 or x 5 7
Write equivalent equations.
x 5 7 or x 5 7
Solve for x.
x 2 or x 12
Simplify.
2
EXAMPLE 1
Solve a simple absolute value equation
ANSWER
The solutions are 2 and 12. These are the values
of x that are 7 units away from 5 on a number
line. The graph is shown below.
3
EXAMPLE 2
Solve an absolute value equation
Solve 5x 10 45.
SOLUTION
5x 10 45
Write original equation.
5x 10 45 or 5x 10 45
Expression can equal 45 or 45 .
5x 55 or 5x 35
Add 10 to each side.
x 11 or x 7
Divide each side by 5.
4
EXAMPLE 2
Solve an absolute value equation
ANSWER
The solutions are 11 and 7. Check these in the
original equation.
Check
5x 10 45
5x 10 45
5
for Examples 1, 2 and 3
GUIDED PRACTICE
Solve the equation. Check for extraneous
solutions.
4. 3x 2 13
6
EXAMPLE 3
Check for extraneous solutions
Solve 2x 12 4x. Check for extraneous
solutions.
SOLUTION
2x 12 4x
Write original equation.
2x 12 4x or 2x 12 4x
Expression can equal 4x or 4 x
12 2x or 12 6x
Add 2x to each side.
6 x or 2 x
Solve for x.
7
for Examples 1, 2 and 3
GUIDED PRACTICE
Solve the equation. Check for extraneous
solutions.
6. 4x 1 2x 9
8
EXAMPLE 3
Check for extraneous solutions
Check the apparent solutions to see if either is
extraneous.
CHECK
2x 12 4x
2x 12 4x
9
for Examples 1, 2 and 3
GUIDED PRACTICE
Solve the equation. Check for extraneous
solutions.
1. x 5
10
for Example 4
GUIDED PRACTICE
Solve the inequality. Then graph the solution.
7. x 4 6
11
EXAMPLE 4
Solve an inequality of the form ax b gt c
Solve 4x 5 gt 13. Then graph the solution.
SOLUTION
Write inequalities.
Subtract 5 from each side.
Divide each side by 4.
12
EXAMPLE 4
Solve an inequality of the form ax b gt c
ANSWER
13
for Examples 1, 2 and 3
GUIDED PRACTICE
Solve the equation. Check for extraneous
solutions.
2. x 3 10
14
for Examples 1, 2 and 3
GUIDED PRACTICE
Solve the equation. Check for extraneous
solutions.
3. x 2 7
15
for Examples 1, 2 and 3
GUIDED PRACTICE
Solve the equation. Check for extraneous
solutions.
5. 2x 5 3x
16
EXAMPLE 5
Solve an inequality of the form ax b c
SOLUTION
17
EXAMPLE 5
Solve an inequality of the form ax b c
w 5.125 0.125
Write inequality.
Write equivalent compound inequality.
0.125 w 5.125 0.125
5 w 5.25
Add 5.125 to each expression.
18
EXAMPLE 6
Write a range as an absolute value inequality
Tolerance 8.25 7.875
0.375
19
for Examples 5 and 6
GUIDED PRACTICE
Solve the inequality. Then graph the solution.
10. x 2 lt 6
The solutions are all real numbers less than 8
or greater than 4. The graph is shown below.
20
for Example 4
GUIDED PRACTICE
Solve the inequality. Then graph the solution.
8. 2x 7gt1
21
for Examples 5 and 6
GUIDED PRACTICE
Solve the inequality. Then graph the solution.
11. 2x 1 9
The solutions are all real numbers less than 5
or greater than 4. The graph is shown below.
22
for Examples 5 and 6
GUIDED PRACTICE
13. Gymnastics For Example 6, write an
absolute value inequality describing the
unacceptable mat thicknesses.
23
for Examples 5 and 6
GUIDED PRACTICE
Solve the inequality. Then graph the solution.
12. 7 x 4
24
for Example 4
GUIDED PRACTICE
Solve the inequality. Then graph the solution.
9. 3x 5 10
25
EXAMPLE 6
Write a range as an absolute value inequality
SOLUTION
26
EXAMPLE 6
Write a range as an absolute value inequality
27
Solving Absolute Value Inequalities
Review
28
Review of the Steps to Solve a Compound
Inequality
- Example
- This is a conjunction because the two inequality
statements are joined by the word and. - You must solve each part of the inequality.
- The graph of the solution of the conjunction is
the intersection of the two inequalities. Both
conditions of the inequalities must be met. - In other words, the solution is wherever the two
inequalities overlap. - If the solution does not overlap, there is no
solution.
29
Review of the Steps to Solve a Compound
Inequality
- Example
- This is a disjunction because the two inequality
statements are joined by the word or. - You must solve each part of the inequality.
- The graph of the solution of the disjunction is
the union of the two inequalities. Only one
condition of the inequality must be met. - In other words, the solution will include each of
the graphed lines. The graphs can go in opposite
directions or towards each other, thus
overlapping. - If the inequalities do overlap, the solution is
all reals.
30
and Statements can be Written in Two Different
Ways
- 1. 8 lt m 6 lt 14
- 2. 8 lt m6 and m6 lt 14
- These inequalities can be solved using two
methods.
31
Method One
- Example 8 lt m 6 lt 14
- Rewrite the compound inequality using the
word and, then solve each inequality. - 8 lt m 6 and m 6 lt 14
- 2 lt m m lt 8
- m gt2 and m lt 8
- 2 lt m lt 8
- Graph the solution
32
Method Two
- Example 8 lt m 6 lt 14
- To solve the inequality, isolate the variable by
subtracting 6 from all 3 parts. - 8 lt m 6 lt 14
- -6 -6 -6
- 2 lt m lt 8
- Graph the solution.
33
or Statements
- Example x - 1 gt 2 or x 3 lt -1
- x gt 3 x lt -4
- x lt -4 or x gt3
- Graph the solution.
34
Solving an Absolute Value Inequality
- Step 1 Rewrite the inequality as a conjunction
or a disjunction. - If you have a you are working with a
conjunction or an and statement. - Remember Less thand
- If you have a you are working with a
disjunction or an or statement. - Remember Greator
- Step 2 In the second equation you must negate
the right hand side and reverse the direction of
the inequality sign. - Solve as a compound inequality.
35
Example 1
- 2x 1 gt 7
- 2x 1 gt 7 or 2x 1 gt7
- 2x 1 gt7 or 2x 1 lt-7
- x gt 3 or x lt -4
This is an or statement. (Greator).
Rewrite. In the 2nd inequality, reverse the
inequality sign and negate the right side
value. Solve each inequality. Graph the solution.
36
Example 2
This is an and statement. (Less thand).
Rewrite. In the 2nd inequality, reverse the
inequality sign and negate the right side
value. Solve each inequality. Graph the
solution.
- x -5lt 3
- x -5lt 3 and x -5lt 3
- x -5lt 3 and x -5gt -3
- x lt 8 and x gt 2
- 2 lt x lt 8