MATH PROBLEM SOLVING

1
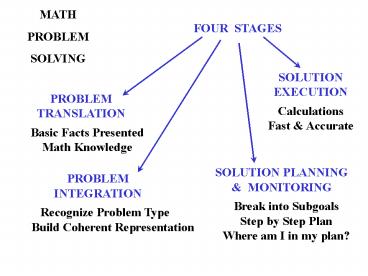
MATH PROBLEM SOLVING
FOUR STAGES
SOLUTION EXECUTION
PROBLEM TRANSLATION
Calculations Fast Accurate
Basic Facts Presented Math Knowledge
SOLUTION PLANNING MONITORING
PROBLEM INTEGRATION
Break into Subgoals Step by Step Plan Where am
I in my plan?
Recognize Problem Type Build Coherent
Representation
2
SAMPLE PROBLEM
Floor tiles are sold in squares 30 cm on
each side. How much would it cost to tile a
rectangular room 7.2 meters long and 5.4 meters
wide if the tile cost .72 each?
ONE POSSIBLE SOLUTION PLAN
Step 1 change width length into number of
tiles 540/30 18 tiles 720/30 24
tiles Step 2 determine how many square tiles
cover the floor 18 times 24 432
tiles Step 3 determine the cost of the 432
tiles 432 times .72 311.04
3
WHAT DO YOU NEED TO KNOW TO SOLVE THE TILE
PROBLEM?
Step 1 Problem Translation Linguistic
Knowledge - need to be able to understand
English sentences in order to recognize the facts
of the problem (What are the givens? What is the
problem goal?) For the tile problem -
room is rectangle, 7.2 by 5.4 meters - each tile
costs .72 - goal is to find total cost of
tiling the room Translation process also
requires factual knowledge about mathematics -
one meter equals 100 cm
4
WHAT DO YOU NEED TO KNOW TO SOLVE THE TILE
PROBLEM?
Step 2 Problem Integration Schematic
Knowledge - need to integrate information into a
coherent representation, need to recognize
problem type For the tile problem -
this is a rectangle problem - need to use the
rectangle area formula to solve the problem
Area length x width Problem
Integration involves more than statement by
statement translation
5
PROBLEM INTEGRATION ENABLES YOU TO RECOGNIZE
INCONSISTENCIES
The number of quarters a man has is seven
times the number of dimes he has. The value of
dimes exceeds the value of the quarters by 2.50.
How many has he of each coin?
WRITE THE EQUATIONS YOU NEED TO SOLVE THE PROBLEM
AND THEN SOLVE!
Q 7 D D (.10) 2.50 Q (.25) Anything
wrong?
6
PROBLEM INTEGRATION ENABLES YOU TO CONSTRUCT A
SITUATION MODEL
Can you give an example of a concrete
situation that corresponds to

3 4
1 2
1
That is, create a simple word problem that could
be solved by the above equation.
Problems of this type were given to elementary
school teachers in the U.S. and China (try to do
this yourself, sample answers - next slide)
7
STUDY ON SITUATION MODELS U.S. vs. CHINESE
TEACHERS
Incorrect model If you have one pie and 3/4 of
another pie to be divided equally by two people,
how much pie will each person get?
Correct model If a team of workers construct
1/2 kilometer of road per day, how many days will
it take them to construct a road 1 and 3/4
kilometers long?
Results 96 of the U.S. teachers either could
not describe an appropriate concrete situation or
produced an incorrect model. 90 of the Chinese
teachers produced correct models. YIKES!!!!!
8
WHICH TWO PROBLEMS BELONG TOGETHER?
1. A personnel expert wishes to determine
whether experienced typists are able to type
faster than inexperienced typists. 20 expert
typists (5 yr or more experience) and 20
inexperienced typists (less than 5 yrs) are given
a typing test. Each typists average number of
words per minute is recorded. 2. A personnel
expert wished to determine whether typing
experience goes with faster typing speeds. 40
typists are asked to report their years of
experience as typists and are given a typing test
to determine their average number of words per
minute. 3. After examining weather data for the
last 50 years, a meteorologist claims that the
annual precipitation varies with average
temperature. For each of 50 years, she notes the
annual rainfall and average temperature.
Experienced math problem solvers pick 2 and
3 Inexperienced math problem solvers pick 1 and 2.
9
CAN THESE PROBLEMS BE SOLVED? ANY IRRELEVANT
INFORMATION?
1. A rectangular lawn is 12 meters long and 5
meters wide. Calculate the area of a path 1.75
meters wide around the lawn. 2. The length of a
rectangular park is 6 meters more than its width.
A walkway 3 meters wide surrounds the park.
Find the dimensions of the park if it has an area
of 432 square meters. 3. The lengths of the
sides of a blackboard are in a 23 ratio. What
is the perimeter (in meters) of the
blackboard? Most high school students make
mistakes on more than half of problems like the
ones shown above.
10
IMPLICATIONS FOR INSTRUCTION TEACHING PROBLEM
INTEGRATION SKILLS

• use varied presentation to encourage students
  to discriminate among problem types
• encourage students to draw diagrams
  
• practice sorting problems into categories
• practice identifying relevant and irrelevant
  information

11
WHAT DO YOU NEED TO KNOW TO SOLVE THE TILE
PROBLEM?
Step 3 Solution Planning and Monitoring
Strategic Knowledge - need general strategies
that can be used to devise and monitor a solution
plan For the tile problem - draw a
picture - work backwards from goal goal is to
find total cost of tiling floor, so
you need to know the of tiles that cover the
floor - divide into subgoals change dimensions
into of tiles, then determine how many tiles
cover the floor, then determine the cost
of all the tiles general strategies are
italicized
7.2 m
5.4 m
12
WHAT DO YOU NEED TO KNOW TO SOLVE THE TILE
PROBLEM?
Step 4 Solution Execution Procedural
Knowledge - computational procedures from simple
procedures (e.g., single digit addition or
subtraction) to more complex procedures (e.g.,
subtraction of multiple digit numbers)
For the tile problem 540/30 18
tiles 720/30 24 tiles 18 x 24 432
tiles 432 times .72 311.04 Key
Point able to do computations with no
difficulty, fast and accurate (achieve
automaticity, direct retrieval from long-term
memory)
13
FAULTY BELIEFS ABOUT MATH THAT UNDERMINE
EFFECTIVE PROBLEM SOLVING
1) Ordinary students cannot expect to understand
math, they have to memorize it, and just apply
what they have learned mechanically and without
understanding. 2) All story problems can be
solved by applying operations suggested by key
words in the story (in all suggests addition,
left suggests subtraction, share suggests
division - 3rd graders) 3) Any assigned problem
should be solved within five minutes or less.
(High school students estimated the typical
problem should take about 2 minutes) 4) Math is
not particularly useful or sensible. Math is
mostly a set of rules and mathematics learning
means memorizing the rules (54 of 4th graders
and 40 of eighth graders females attitudes
toward math more negative).
14
ATTRIBTUTION STYLE UNDERMINES EFFECTIVE MATH
PROBLEM SOLVING
Researchers gave 10 year old children a
questionnaire asking about their likely reactions
to hypothetical failures. They identified two
attribution styles Mastery-oriented
likely to think they should work harder in the
face of failure/difficulty Helpless likely
to respond to difficulty with negative
attributions about ability There were no IQ
differences between these two groups. Many
more girls were categorized as helpless.
15
ATTRIBTUTION STYLE UNDERMINES EFFECTIVE MATH
PROBLEM SOLVING - CONTINUED
Researchers next gave the children a series of
confusing math problems (difficult to solve), and
then a batch of easy math problems (that all
children should be able to solve). What
happened? Mastery-oriented children These
children were able to recoup from the negative
experience and solved the easy problems with
ease. Helpless These children were thrown
by the confusing problems and didnt try very
hard on the easy problems, getting many of them
wrong.
16
ATTRIBTUTION STYLE UNDERMINES EFFECTIVE MATH
PROBLEM SOLVING - CONTINUED
Researchers wanted to know why girls were more
likely to adopt a helpless attribution style.
What happens in the classroom? Boys and
girls receive the same amount of negative
comments. But the nature of these comments
differ. Boys Criticisms sometimes
focus on intellectual quality, sometimes on
neatness, conduct, or effort. Boys and girls
both think teachers like girls better.
Girls Teacher criticisms focus consistently on
the intellectual quality of the work. End Result
Boys attribute failure to any number of factors,
girls are left with negative attributions
concerning their ability.