M

1
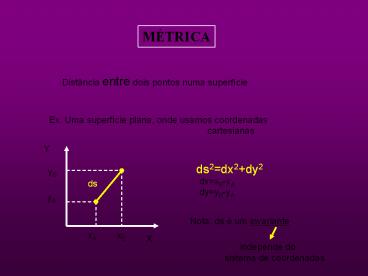
MÉTRICA
Distância entre dois pontos numa superfície
Ex. Uma superfície plana, onde usamos coordenadas

cartesianas
ds2dx2dy2
dxxB-xA dyyB-yA
Nota ds é um invariante
independe do sistema de coordenadas
2
Fazendo uma transformação de coordenadas
(x,y) ? (x1,x2)
x e y combinações de x1 e x2 x x(x1,x2) y
y(x1,x2)
Uma mudança dx em x resulta em mudanças dx1 e dx2
( o mesmo para y )
ds2dx2dy2
3
Escrevendo a equação de forma mais compactada
distância entre 2 pontos próximos sobre uma
superfície
tensor métrico
representação da distância em ? coordenadas
4
EXEMPLOS
Métrica euclidiana
matriz unidade
ds2dx2dy2
Coordenadas polares no plano
(x,y) ? (r,?)
x r cos? y r sin?
Calculando os gr? ?
métrica euclidiana em coordenadas polares
ds2dr2r2d?2
5
Determinação de K através da métrica
Seja x1 e x2 um sistema de coordenadas arbitrário
sobre uma superfície ?
distância entre dois pontos vizinhos
Pode-se demonstrar que, com uma mudança de
coordenadas conveniente, o tensor métrico pode
ser representado por uma matriz diagonal
6
Define-se então a métrica ortogonal
ds2g11(x1,x2)dx12g22(x1,x2)dx22
TEOREMA EGREGIUM DE GAUSS
Demonstrou que se pode derivar a K de uma
superfície arbitrária somente conhecendo a forma
que os coeficientes da métrica variam de um ponto
a outro, não importando o valor absoluto destes
coeficientes com o sistema de coordenadas
escolhido
Conhecendo-se a métrica ortogonal de uma
superfície determina-se a sua curvatura.

• K é um invariante
• que seja o sistema de coordenadas
• K tem o mesmo valor num dado
• ponto numa superfície

7
EXEMPLOS
Plano
ds2dx2dy2
K 0
Cilindro
Coordenadas cilíndricas x R cos? (pontos na
superfície) y R sin?
z z
nota zx e R?y ds2dx2dy2
ds2dz2R2d?2
Usando gauss ? K 0
métrica euclidiana!!!
8
Esfera
x R sin? cos? y R sin? sin? z R cos?
ds2R2 d?2R2 sin2? d?2
Usando o teorema de gauss
K 1/R2
Não há nenhuma transformação de coordenadas que
leve a sua métrica a uma do tipo euclidiana
esfera intrinsecamente curva
9
Determinação de perímetros e áreas de círculos
geodésicos desenhados sobre uma superfície usando
a métrica
Círculo sobre uma superfície plana
elemento de arco
Métrica ds2dr2r2d?2 (coordenadas polares)

• elemento de arco (rR fixo) ? dsR d? ? C?ds
  2?R

Se a métrica for ortogonal (g12g210), o
elemento de área sobre uma superfície é dado
por

• então dArdrd? ? A ?dA

?R2
10
Círculo de raio r sobre uma superfície esférica
r raio próprio do círculo
Métrica ds2R2d?2R2sin2?d?2

• perímetro do círculo de raio r fixo ? d?0
• ? ds R sin? d?

C?ds2?Rsin?2?Rsin(r/R)
arco rR?

• área do círculo

A2?R2(1-cosr/R)