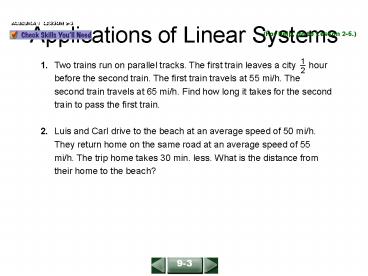
Applications of Linear Systems

1
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
(For help, go to Lesson 2-5.)
1 2
1. Two trains run on parallel tracks. The first
train leaves a city hour before the second
train. The first train travels at 55 mi/h. The
second train travels at 65 mi/h. Find how long it
takes for the second train to pass the first
train. 2. Luis and Carl drive to the beach at
an average speed of 50 mi/h. They return home on
the same road at an average speed of 55 mi/h. The
trip home takes 30 min. less. What is the
distance from their home to the beach?
9-3
2
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
1. 55t 65(t 0.5) 55t 65t
32.5 32.5 10t 3.25 t It takes 3.25
hours for the second train to pass the first
train. 2. 50t 55(t 0.5) 50t 55t
27.5 27.5 5t 5.5 t 50t 50(5.5)
275 It is 275 miles to the beach from their home.
Solutions
9-3
3
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
A chemist has one solution that is 50 acid. She
has another solution that is 25 acid. How many
liters of each type of acid solution should she
combine to get 10 liters of a 40 acid solution?
Step 1 Choose one of the equations and solve for
a variable. a b 10 Solve for a.
a 10 b Subtract b from each side.
9-3
4
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
(continued)
Step 2 Find b. 0.5a 0.25b
0.4(10) 0.5(10 b) 0.25b
0.4(10) Substitute 10 b for a. Use
parentheses. 5 0.5b 0.25b
0.4(10) Use the Distributive Property.
5 0.25b 4 Simplify.
0.25b 1 Subtract 5 from each
side. b 4
Divide each side by 0.25.
Step 3 Find a. Substitute 4 for b in either
equation. a 4 10
a 10 4 a 6
To make 10 L of 40 acid solution, you need 6 L
of 50 solution and 4 L of 25 solution.
9-3
5
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
Suppose you have a typing service. You buy a
personal computer for 1750 on which to do your
typing. You charge 5.50 per page for typing.
Expenses are .50 per page for ink, paper,
electricity, and other expenses. How many pages
must you type to break even?
9-3
6
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
(continued)
Choose a method to solve this system. Use
substitution since it is easy to substitute for d
with these equations.
d 0.5p 1750 Start with one equation.
5.5p 0.5p 1750 Substitute 5.5p for
d. 5p 1750 Solve for p. p
350
To break even, you must type 350 pages.
9-3
7
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
Suppose it takes you 6.8 hours to fly about 2800
miles from Miami, Florida to Seattle, Washington.
At the same time, your friend flies from Seattle
to Miami. His plane travels with the same average
airspeed, but this flight only takes 5.6 hours.
Find the average airspeed of the planes. Find the
average wind speed.
9-3
8
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
(continued)
Step 2 Solve for A. A 456 Divide
each side by 2.
Step 3 Solve for W using either of the original
equations. A W 500 Use the first
equation. 456 W 500 Substitute 456
for A. W 44 Solve for W.
The average airspeed of the planes is 456 mi/h.
The average wind speed is 44 mi/h.
9-3
9
Applications of Linear Systems
ALGEBRA 1 LESSON 9-3
1. One antifreeze solution is 10 alcohol.
Another antifreeze solution is 18 alcohol. How
many liters of each antifreeze solution should be
combined to create 20 liters of antifreeze
solution that is 15 alcohol? 2. A local band
is planning to make a compact disk. It will cost
12,500 to record and produce a master copy,
and an additional 2.50 to make each sale copy.
If they plan to sell the final product for 7.50,
how many disks must they sell to break
even? 3. Suppose it takes you and a friend 3.2
hours to canoe 12 miles downstream (with the
current). During the return trip, it takes you
and your friend 4.8 hours to paddle upstream
(against the current) to the original starting
point. Find the average paddling speed in still
water of you and your friend and the average
speed of the current of the river. Round
answers to the nearest tenth.
7.5 L of 10 solution 12.5 L of 18 solution
2500 disks
still water 3.1 mi/h current 0.6 mi/h
9-3