Optimizing Flocking Controllers using Gradient Descent

1
Optimizing Flocking Controllers using Gradient
Descent
Kevin Forbes
2
Motivation

• Flocking models can animate complex scenes in a
  cost-effective way
• But, they are hard to control there are many
  parameters that interact in non-intuitive ways
  animators find good values by trial and error

• Can we use machine learning techniques to
  optimize the parameters instead of setting them
  by hand?

3
Background Flocking model
Reynolds (1987) Flocks, Herds, and Schools A
Distributed Behavioral Model Reynolds (1999)
Steering Behaviors For Autonomous Characters

• Each agent can see other agents in its
  neighbourhood
• Motion derived from weighted combination of
  force vectors

Alignment
Cohesion
Separation
4
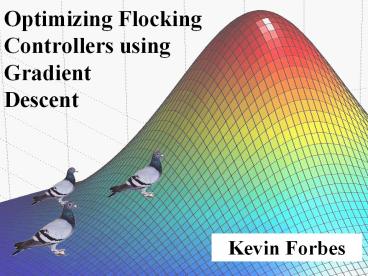
Background Learning Model
Lawrence (2003) Efficient Gradient Estimation
for Motor Control Learning
Policy Search Finds optimal settings of a
systems control parameter vector, as evaluated
by some objective function Stochastic elements in
the system result in noisy gradient estimates,
but there are techniques to limit their effects.
Simple 2-parameter example Axes values of
control parameters Color value of objective
function Blue arrows negative gradient of
objective function Red line result of gradient
descent
5
Project Steps

1. Define physical agent model
2. Define flocking forces
3. Define objective function
4. Take derivatives of all system element w.r.t all
   control parameters
5. Do policy search

6
1. Agent Model
Position, Velocity and Acceleration defined as in
Reynolds (1999)
Recursive definition the base case is the
systems initial condition. If there are no
stochastic forces, the system is deterministic
(w.r.t. the initial conditions). The flocks
policy is defined by the alpha vector.

7
2. Forces
The simulator includes the following
forces Flocking Forces Cohesion,
Separation, Alignment Single-Agent
Forces Noise, Drag Environmental
Forces Obstacle Avoidance, Goal Seeking
Implemented with learnable coefficients (so far)
8
3. Objective Function
The exact function used depends upon the goals of
the particular animation I used the following
objective function for the flock at time t
The neighbourhood function implied here (and in
the force calculations) will come back to haunt
us on the next slide. . .

9
4. Derivatives
In order to estimate the gradient of the
objective function, it must be differentiable.
We can build an appropriate N-function by
multiplying transformed sigmoids together

• Other derivative-related wrinkles
• Can not use max/min truncations
• Numerical stability issues
• Increased memory requirements

10
5. Policy Search
Use Monte Carlo to estimate the expected value of
the gradient
This assumes that the only random variables are
the initial conditions. A less-noisy estimate can
be made if the distribution of the stochastic
forces in the model are taken into account using
importance sampling.
11
The Simulator

• Features
• Forward flocking simulation
• Policy learning and mapping
• Optional OpenGL visualization
• Spatial sorting gives good performance

• Limitations
• Wraparound
• Not all forces are learnable yet
• Buggy neighbourhood function derivative

12
Experimental Method

• Simple Gradient descent
• Initialize flock, assign a random alpha
• Run simulation ( N times)
• Step (with annealing) in negative gradient
  direction
• Reset flock
• Steps 2-4 are repeated for a certain number of
  steps

13
Results - ia

• Simple system test
• 1 agent
• 2 forces seek and drag
• Seek target in front of agent agent initially
  moving towards target
• Simulate 2 minutes
• No noise
• Take best of 10 descents

14
Results - ib

• Simple system test w/noise
• Same as before, but set the wander force to
  strength 1
• Used N10 for the Monte Carlo estimate

• Effects of noise
• Optimal seek force is larger
• Both surface and descent path are noisy

15
Results - ii

• More complicated system
• 2 Agents
• Seek and drag set at 10, .1
• Learn cohesion, separation
• Seek target orbiting agents start position
• Simulate 2 minutes
• Target distance of 5,10
• Noise in initial conditions

• Results
• Target distance does influence the optimized
  values
• Search often gets caught in foothills

16
Results - iii

• Higher dimensions
• 10 agents
• Learn cohesion, separation, seek, drag
• Otherwise the same as last test

• Results
• Objective function is being optimized (albeit
  slowly)!
• Target distance is matched!

17
Conclusion

• Technique shows promise
• Implementation has poor search performance

Future Work

• Implement more learnable parameters
• Fix neighbourhood derivative
• Improve gradient search method
• Use importance sampling!

Demonstrations