RTL Design Flow - PowerPoint PPT Presentation
Title:
RTL Design Flow
Description:
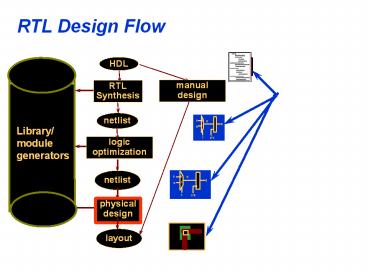
RTL Design Flow HDL manual design RTL Synthesis netlist a 0 d q Library/ module generators 1 b s clk logic optimization netlist a 0 d q 1 b s clk physical design layout – PowerPoint PPT presentation
Number of Views:226
Avg rating:3.0/5.0
Title: RTL Design Flow
1
RTL Design Flow
HDL
manual design
RTL Synthesis
netlist
logic optimization
netlist
physical design
layout
2
Physical Design Overall Conceptual Flow
Input
Read Netlist
Floorplanning
Floorplanning
Initial Placement
Placement
Routing
Compaction/clean-up
Output
Write Layout Database
3
Results of Placement
A good placement
A bad placement
Whats good about a good placement? Whats bad
about a bad placement?
A. Kahng
4
Results of Placement
- Good placement
- Circuit area (cost) and wiring decreases
- Shorter wires ? less capacitance
- Shorter delay
- Less dynamic power dissipation
- Bad placement causes routing congestion
resulting in - Increases in circuit area (cost) and wiring
- Longer wires ? more capacitance
- Longer delay
- Higher dynamic power dissipation
5
Gordian Placement Flow
module coordinates
Global Optimization minimization of
wire length
Partitioning of the module set and
dissection of the placement region
position constraints
Regions with ? k modules
module coordinates
Final Placement adoption
of style dependent constraints
Data flow in the placement procedure GORDIAN
Complexity space O(m) time Q( m1.5
log2m) Final placement standard cell
macro-cell SOG
6
Gordian A Quadratic Placement Approach
- Global optimization
solves a sequence of quadratic programming
problems - Partitioning
enforces the non-overlap constraints
7
Intuitive formulation
- Given a series of points x1, x2, x3, xn
- and a connectivity matrix C describing the
connections between them - (If cij 1 there is a connection between xi and
xj) - Find a location for each xj that minimizes the
total sum of all spring tensions between each
pair ltxi, xjgt
Problem has an obvious (trivial) solution what
is it?
8
Improving the intuitive formulation
- To avoid the trivial solution add constraints
Hxb - These may be very natural - e.g. endpoints (pads)
- To integrate the notion of critical nets
- Add weights wij to nets
x1
xn
wij - some springs have more tension should pull
associated vertices closer
wij
9
Modeling the Nets Wire Length
connection to other modules
y
module u
net node
v
l
vu
(xu ,yu )
h
x
)
,
(
vu
vu
(xv ,yv)
x
The length Lv of a net v is measured by the
squared distances from its points to the nets
center
å
(
)
(
)
2
2
-
-
y
y
x
x
L
v
v
uv
v
uv
u
?
M
v
( x
y
yu
y )
xu
x
uv
uv
uv
vu
10
Toy Example
x100
x200
x1
- x2
D. Pan
11
Quadratic Optimization Problem
D
G
F
E
D
C
B
A
E
ù
é
M
M
M
M
M
M
M
M
)
(
v
u
,
r
r
'
'
ú
ê
F
r
0
0
0
L
ú
ê
)
(
l
A
B
ú
ê
'
r
0
0
0
L
A
ú
ê
)
(
v
u
,
r
r
û
ë
M
M
M
M
M
M
M
M
C
- Linearly constrained quadratic programming problem
T
T
F
)
(
min
x
d
x
C
x
x
Accounts for fixed modules
m
Î
R
x
Wire-length for movable modules
)
(
)
(
l
l
s.t.
u
x
A
Center-of-gravity constraints
Problem is computationally tractable, and well
behaved Commercial solvers available mostek
12
Global Optimization Using Quadratic Placement
- Quadratic placement clumps cells in center
- Partitioning divides cells into two regions
- Placement region is also divided into two regions
- New center-of-gravity constraints are added to
the constraint matrix to be used on the next
level of global optimization - Global connectivity is still conserved
13
Setting up Global Optimization
14
Layout After Global Optimization
A. Kahng
15
Partitioning
16
Partitioning
- In GORDIAN, partitioning is used to constrain the
movement of modules rather than reduce problem
size - By performing partitioning, we can iteratively
impose a new set of constraints on the global
optimization problem - Assign modules to a particular block
- Partitioning is determined by
- Results of global placement initial starting
point - Spatial (x,y) distribution of modules
- Partitioning cost
- Want a min-cut partition
17
Layout after Min-cut
Now global placement problem will be solved again
with two additional center_of_gravity constraints
18
Adding Positioning Constraints
- Partitioning gives us two new center of
gravity constraints - Simply update constraint matrix
- Still a single global optimization problem
- Partitioning is not absolute
- modules can migrate back during optimization
- may need to re-partition
19
Continue to Iterate
20
First Iteration
A. Kahng
21
Second Iteration
A. Kahng
22
Third Iteration
A. Kahng
23
Fourth Iteration
A. Kahng
24
Final Placement
25
Final Placement - 1
- Earlier steps have broken down the problem into a
manageable number of objects - Two approaches
- Final placement for standard cells/gate array
row assignment - Final placement for large, irregularly sized
macro-blocks slicing wont talk about this
26
Final Placement Standard Cell Designs
A. E. Dunlop, B. W. Kernighan, A procedure for
placement of standard-cell VLSI circuits, IEEE
Trans. on CAD, Vol. CAD-4, Jan , 1985, pp. 92- 98
27
Final Placement Creating Rows
1
1
1
1,2
1,2
1,2
1,2
2
2
2,3
2,3
Row-based standard cell design
2,3
2,3
3
3
3
3,4
3,4
3,4
3,4
4
4
4
4
4,5
4,5
5
5
5
5
5
5
Partitioning of circuit into 32 groups. Each
group is either assigned to a single row or
divided into 2 rows
28
Standard Cell Layout
29
Another Series of Gordian
(a) Global placement with 1 region
(b) Global placement with 4 region
(c) Final placements
D. Pan U of Texas