Pr - PowerPoint PPT Presentation
Title: Pr
1
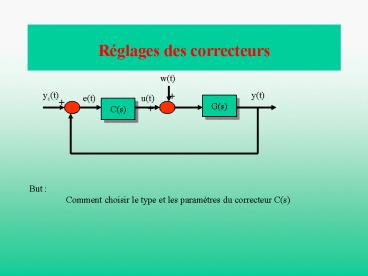
Réglages des correcteurs
But Comment choisir le type et les paramètres
du correcteur C(s)
2
Méthode de Naslin
But Paramétrer les correcteurs en garantissant
à la réponse indicielle un D
On considère la FTBF
Le D sera garanti ssi
3
Méthode de Naslin
(ep0 et ev0)
Si la FTBF
Le D sera garanti ssi
(ep?0 et ev?0)
Si la FTBF
Le D sera garanti ssi
4
Méthode de Naslin
Mode demploi - Calculer la FTBF - Calculer
a - Calculer - Vérifier les conditions sans
tenir compte du numérateur. - Calculer ac. Si
acf(param correc), prendre les valeurs
limites des paramètres (ac est constant). -
Vérifier les conditions par rapport à ac.
Exemple
Comment choisir Kp et Ti pour garantir un D lt
10 et une ep0
5
Méthode de Ziegler Nichols
Réglage par génération des oscillations entretenue
G(t)
y(t)
G(s)
K
-
- On annule totalement les actions I et D .
- On augmente progressivement laction du P jusquà
lapparition - des oscillations entretenues.
- On note la valeur critique du gain Kc et on
mesure la période dosci Tosc. - - Suivant le type de réglage choisi, les réglages
recommandés sont
Correcteur P KP 0.5 Kc
Correcteur PI KP 0.45 Kc, Ti 0.85 Tosc
Correcteur PID KP 0.6 Kc, Ti0.5Tosc , Td
0.12 Tosc
6
Méthode de Ziegler et Nichols
- On trace la réponse indicielle de G(s)
- On trace la tangente qui passe par le
- point dinflexion.
- On calcule les paramètres t et k de
7
Méthode de Graham-Lathrop
Les auteurs ont cherché par simulation les FTBF
F(s) à écart permanent nul en minimisant le
critère J e(t) désigne lécart dasservissement
pour une entrée échelon .
yc
min
F(s)
t
-
8
Méthode de Graham-Lathrop
Ep0 et Ev?0 Ep0 et Ev 0
1
2
3
4
9
Méthode de Prédicteur de Smith
FTBF
10
Méthode de Prédicteur de Smith
Consigne
Sortie
C(s)
e-ts
G1(s)
-
Le correcteur C(s) peut être déterminé de façon
classique pour compenser G1(s). La sortie
conserve nécessairement un retard sur la consigne
11
Réglage par compensation
Réglage PD dun intégrateur pur avec retard
Le choix dune action dérivée provoquant une
avance de phase de p/4 pour la pulsation w0 de w
déterminant un déphasage de p.
C-à-d arctg(Tdw0)p/4 quand j(wà)-p
12
Tdw01
-p-p/2p/4-tw0
C(jw)G(jw)1
Si on veut Mg6 dB alors kp1kp/2
Si on veut Mg14 dB alors kp2kp/5
Réglage PI dun premier ordre
Si TiT
Si on veut une constante de temps T1
13
Réglage PI dun premier ordre avec retard
Si TiT
jtw-p/2
Mg6dB
Si on veut une marge de gain de 6 dB
j-p
Réglage PID dun premier ordre avec retard
Si TiT
Pour Mggt6dB
Équivalent au 1 cas
14
Réglage PI dun second ordre apériodique
Si T2Ti
BO
FTBF
Pour x donné, on peut calculer kp
15
Réglage PID dun premier ordre avec retard
Si Ti TdT
Pour un D désiré , on calcule x , ensuite on
peut déterminer kp
Réglage PI dun système dordre n avec pôle
dominant
Le pôle dominant est 1/T1 c-à-d T1? 4?Ti 4T?
Une étude heuristique a montré que le choix dun
régulateur PI avec et donne des résultats
satisfaisants