Table-driven parsing - PowerPoint PPT Presentation
1 / 22
Title:
Table-driven parsing
Description:
Table-driven parsing Parsing performed by a finite state machine. Parsing algorithm is language-independent. FSM driven by table (s) generated automatically from grammar. – PowerPoint PPT presentation
Number of Views:58
Avg rating:3.0/5.0
Title: Table-driven parsing
1
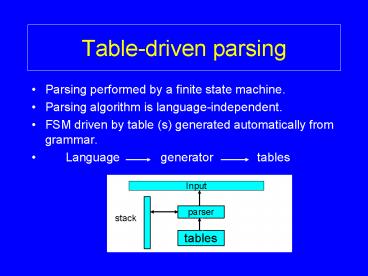
Table-driven parsing
- Parsing performed by a finite state machine.
- Parsing algorithm is language-independent.
- FSM driven by table (s) generated automatically
from grammar. - Language generator
tables
Input
parser
stack
tables
2
Pushdown Automata
- A context-free grammar can be recognized by a
finite state machine with a stack a PDA. - The PDA is defined by set of internal states and
a transition table. - The PDA can read the input and read/write on the
stack. - The actions of the PDA are determined by its
current state, the current top of the stack, and
the current input symbol. - There are three distinguished states
- start state nothing seen
- accept state sentence complete
- error state current symbol doesnt belong.
3
Top-down parsing
- Parse tree is synthesized from the root (sentence
symbol). - Stack contains symbols of rhs of current
production, and pending non-terminals. - Automaton is trivial (no need for explicit
states) - Transition table indexed by grammar symbol G and
input symbol a. Entries in table are terminals or
productions P ABC
4
Top-down parsing
- Actions
- initially, stack contains sentence symbol
- At each step, let S be symbol on top of stack,
and a be the next token on input. - if T (S, a) is terminal a, read token, pop symbol
from stack - if T (S, a) is production P ABC.,
remove S from stack, push the symbols A, B, C on
the stack (A on top). - If S is the sentence symbol and a is the end of
file, accept. - If T (S, a) is undefined, signal error.
- Semantic action when starting a production,
build tree node for non-terminal, attach to
parent.
5
Table-driven parsing and recursive descent parsing
- Recursive descent every production is a
procedure. Call stack holds active procedures
corresponding to pending non-terminals. - Stack still needed for context-sensitive legality
checks, error messages, etc. - Table-driven parser recursion simulated with
explicit stack.
6
Building the parse table
- Define two functions on the symbols of the
grammar FIRST and FOLLOW. - For a non-terminal N, FIRST (N) is the set of
terminal symbols that can start any derivation
from N. - First (If_Statement) if
- First (Expr) id, (
- FOLLOW (N) is the set of terminals that can
appear after a string derived from N - Follow (Expr) , ),
7
Computing FIRST (N)
- If N e First (N) includes e
- if N aABC First (N) includes a
- if N X1X2 First (N) includes First
(X1) - if N X1X2 and X1 e,
- First (N) includes
First (X2) - Obvious generalization to First (a) where a is
X1X2...
8
Computing First (N)
- Grammar for expressions, without left-recursion
- E TE T
- E TE e
- T FT F
- T FT e
- F id (E)
- First (F) id, (
- First (T) , e First (T)
id, ( - First (E) , e First (E)
id, (
9
Computing Follow (N)
- Follow (N) is computed from productions in which
N appears on the rhs - For the sentence symbol S, Follow (S) includes
- if A a N b, Follow (N) includes First
(b) - because an expansion of N will be followed by an
expansion from b - if A a N, Follow (N) includes Follow
(A) - because N will be expanded in the context in
which A is expanded - if A a N B , B e, Follow (N) includes
Follow (A)
10
Computing Follow (N)
- E TE T
- E TE e
- T FT F
- T FT e
- F id (E)
- Follow (E) ), Follow (E) ),
- Follow (T) First (E ) Follow (E) , ),
- Follow (T) Follow (T) , ),
- Follow (F) First (T) Follow (T) , ,
),
11
Building LL (1) parse tables
- Table indexed by non-terminal and token. Table
entry is a production - for each production P A a loop
- for each terminal a in First (a) loop
- T (A, a) P
- end loop
- if e in First (a), then
- for each terminal b in Follow (a) loop
T (A, b) P end loop - end if
- end loop
- All other entries are errors.
- If two assignments conflict, parse table cannot
be built.
12
LL (1) grammars
- If table construction is successful, grammar is
LL (1) left-to right, leftmost derivation with
one-token lookahead. - If construction fails, can conceive of LL (2),
etc. - Ambiguous grammars are never LL (k)
- If a terminal is in First for two different
productions of A, the grammar cannot be LL (1). - Grammars with left-recursion are never LL (k)
- Some useful constructs are not LL (k)
13
Bottom-up parsing
- Synthesize tree from fragments
- Automaton performs two actions
- shift push next symbol on stack
- reduce replace symbols on stack
- Automaton synthesizes (reduces) when end of a
production is recognized - States of automaton encode synthesis so far, and
expectation of pending non-terminals - Automaton has potentially large set of states
- Technique more general than LL (k)
14
LR (k) parsing
- Left-to-right, rightmost derivation with k-token
lookahead. - Most general parsing technique for deterministic
grammars. - In general, not practical tables too large
(106 states for C, Ada). - Common subsets SLR, LALR (1).
15
The states of the LR(0) automaton
- An item is a point within a production,
indicating that part of the production has been
recognized - A a . B b ,
- seen the expansion of a, expect to see expansion
of B - A state is a set of items
- Transition within states are determined by
terminals and non-terminals - Parsing tables are built from automaton
- action shift / reduce depending on next symbol
- goto change state depending on synthesized
non-terminal
16
Building LR (0) states
- If a state includes
- A a . B b
- it also includes every state that is the start of
B - B . X Y Z
- Informally if I expect to see B next, I expect
to see anything that B can start with, and so on - X . G H I
- States are built by closure from individual items.
17
A grammar of expressions initial state
- E E
- E E T T -- left-recursion ok
here. - T T F F
- F id (E)
- S0 E .E, E .E T, E .T,
- F .id, F . ( E )
, - T .T F, T .F
18
Adding states
- If a state has item A a .a b,
- and the next symbol in the input is a, we
shift a on the stack and enter a state that
contains item - A a a.b
- (as well as all other items brought in by
closure) - if a state has as item A a. , this
indicates the end of a production reduce action.
- If a state has an item A a .N b, then
after a reduction that find an N, go to a state
with A a N. b
19
The LR (0) states for expressions
- S1 E E., E E. T
- S2 E T., T T. F
- S3 T F.
- S4 F (. E), S0 (by closure)
- S5 F id.
- S6 E E . T, T .T F, T .F, F
.id, F .(E) - S7 T T . F, F .id, F .(E)
- S8 F (E.), E E. T
- S9 E E T., T T. F
- S10 T T F., S11 F
(E).
20
Building SLR tables
- An arc between two states labeled with a terminal
is a shift action. - An arc between two states labeled with a
non-terminal is a goto action. - if a state contains an item A a. , (a
reduce item) - the action is to reduce by this production, for
all terminals in Follow (A). - If there are shift-reduce conflicts or
reduce-reduce conflicts, more elaborate
techniques are needed.
21
LR (k) parsing
- Canonical LR (1) annotate each item with its own
follow set - (A -gt a a.b , f )
- f is a subset of the follow set of A, because it
is derived from a single specific production for
A - A state that includes A -gt a a.b is a reduce
state only if next symbol is in f fewer reduce
actions, fewer conflicts, technique is more
powerful than SLR (1) - Generalization use sequences of k symbols in f
- Disadvantage state explosion impractical in
general, even for LR (1)
22
LALR (1)
- Compute follow set for a small set of items
- Tables no bigger than SLR (1)
- Same power as LR (1), slightly worse error
diagnostics - Incorporated into yacc, bison, etc.