Quadratic Functions and their Graphs

1
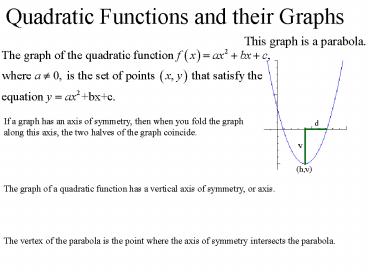
Quadratic Functions and their Graphs
If a graph has an axis of symmetry, then when you
fold the graph along this axis, the two halves of
the graph coincide.
The graph of a quadratic function has a vertical
axis of symmetry, or axis.
The vertex of the parabola is the point where the
axis of symmetry intersects the parabola.
2
(No Transcript)
3
(No Transcript)
4
(No Transcript)
5
To sketch the graph of

• Decide if it opens up or down and the number of
  x-intercepts
• Find the axis and vertex
• Find the x- and y-intercepts

6
Ex. 1. Sketch the parabola
. Label the intercepts, axis of
symmetry, and vertex.
Does it open up or down?
Find the axis
To find the vertex, plug in 2 for x and determine
the y-coordinate.
Find the x and y-intercepts
7
(No Transcript)
8

• Ex. 2.
• Find the vertex of the parabola
  by completing the square.
• Find the x- and y-intercepts

a. Put in vertex form
where (h, k)is the vertex
The vertex is (3, 22)
9
b. When x 0, y 4. So the y-intercept is (0, 4)
To find the x-intercept, let y 0
10
Ex. 3. Where does the line y 3x 5 intersect
the parabola
Set and solve for x
Substitute these into y 3x 5 to get y -7
and y 8 So the intersection points are (-4, -7)
and (1, 8)
Graph to confirm your answer
11
Ex. 4. Find an equation of the function whose
graph is a parabola with x-intercepts (3, 0) and
(6, 0) and y-intercept (0, -2).
If x 3 and x 6 are solutions of this
equation, then (x 3) and (x 6) are factors of
the equation so
Use the y-intercept
Graph to confirm