6.7: Coordinate Proofs

1
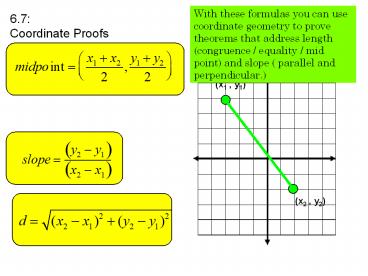
6.7Coordinate Proofs
With these formulas you can use coordinate
geometry to prove theorems that address length
(congruence / equality / mid point) and slope (
parallel and perpendicular.)
(x1 , y1)
(x2 , y2)
2
Examine trapezoid TRAP. Explain why you can
assign the same y-coordinate to points R and A.
The y-coordinates of all points on a horizontal
line are the same, so points R and A have the
same y-coordinates.
6-7
3
Use coordinate geometry to prove that the
quadrilateral formed by connecting the midpoints
of rhombus ABCD is a rectangle.
midpoint midpoint formula
From Lesson 6-6, you know that XYZW is a
parallelogram.
If the diagonals of a parallelogram are
congruent, then the parallelogram is a rectangle
by Theorem 6-14.
congruent distance formula
6-7
4
(continued)
Because the diagonals are congruent,
parallelogram XYZW is a rectangle.
6-7
5
Coordinate Proofs
Prove the midsegment of a trapezoid is parallel
to the base.
(b,c)
(d,c)
The bases are horizontal line with a slope equal
to zero. Is this true for the midsegment?
(0,0)
(a,0)
Conclusion The midsegment of a trapezoid is
parallel to the two bases!
6
Coordinate Proofs
With some experience, you will begin to see the
advantage of using the following coordinates
(2b,2c)
(2d,2c)
(0,0)
(2a,0)
7
Coordinate Proofs
Prove the midsegment of a trapezoid is equal to
half the sum of the two bases.
(2b,2c)
(2d,2c)
(0,0)
(2a,0)
1/2 (2a2d-2b) a d - b d a - b
8
2. Prove that the diagonals of a parallelogram
bisect each other
If the diagonals BISECT, then they will have THE
SAME midpoint.
(2b,2c)
(2b2a,2c)
B
C
D
A
E
(0,0)
(2a,0)
Since the diagonals have the same midpoint, they
bisect each other!
9
Homework 6.7
Page 333 Due at the beginning of the next class.
Name Section Page
Remember the honor code. No Copying!
Show your work here IN PENCIL
I pledge that I have neither given nor received
aid on this assignment
10
GEOMETRY LESSON 6-7
Check in INK!
6-7
11
GEOMETRY LESSON 6-7
Check in INK!
6-7
12
GEOMETRY LESSON 6-7
Check in INK!
6-7
13
GEOMETRY LESSON 6-7
Check in INK!
12 n
12 n
17. no may need measures 18. yes prod. of
slopes of sides of A 1 19. yes Dist.
Formula 20. yes Dist. Formula, 2 sides
21. no may need measures 22. yes
intersection pt. for all 3 segments
23. yes slope of AB slope of BC 24. yes
Dist. Formula, AB BC CD AD 25. 1, 4,
7 26. 0, 2, 4, 6, 8 27. 0.8, 0.4, 1.6, 2.8,
4, 5.2, 6.4, 7.6, 8.8 28. 1.76, 1.52,
1.28, . . . , 9.52, 9.76
29. 2 , 2 2 , 2 3 , .
. . . , 2 (n 1) 30. (0, 7.5), (3, 10),
(6, 12.5) 31. 1, 6 , 1, 8 , (3,
10), 5, 11 , 7, 13 32. (1.8, 6), (0.6,
7),
12 n
12 n
2 3
1 3
2 3
1 3
6-7