KVALITATIV ANALYS - FACKVERK

1
Byggnadsmekanik gk 11.1
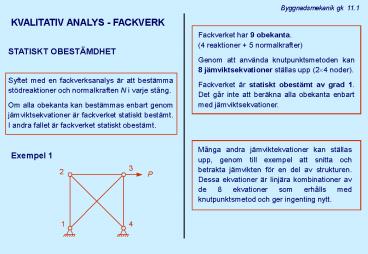
KVALITATIV ANALYS - FACKVERK
Fackverket har 9 obekanta. (4 reaktioner 5
normalkrafter) Genom att använda
knutpunktsmetoden kan 8 jämviktsekvationer
ställas upp (2?4 noder). Fackverket är statiskt
obestämt av grad 1. Det går inte att beräkna alla
obekanta enbart med jämviktsekvationer.
STATISKT OBESTÄMDHET
Syftet med en fackverksanalys är att bestämma
stödreaktioner och normalkraften N i varje
stång. Om alla obekanta kan bestämmas enbart
genom jämviktsekvationer är fackverket statiskt
bestämt. I andra fallet är fackverket statiskt
obestämt.
Många andra jämviktekvationer kan ställas upp,
genom till exempel att snitta och betrakta
jämvikten för en del av strukturen. Dessa
ekvationer är linjära kombinationer av de 8
ekvationer som erhålls med knutpunktsmetod och
ger ingenting nytt.
Exempel 1
2
Byggnadsmekanik gk 11.2
Exempel 2
Exempel 3
8 ekvationer 8 obekanta Statiskt bestämt
antal obekanta 3 reaktioner 6 stänger
9 antal ekvationer 2 ? antal noder 2 ? 4
8 Fackverket är statiskt obestämt av grad 1.
Exempel 4
8 ekvationer 7 obekanta Mekanism
De 3 stödreaktionerna kan bestämmas genom att
betrakta jämvikten av hela strukturen. Strukturen
är yttre statiskt bestämd.
(strukturen kan inte motstå kraften P. Punkt 4
rullar åt höger)
3
Byggnadsmekanik gk 11.3
KVALITATIV ANALYS
Exempel 1
Syftet med kvalitativ analys av ett fackverk är
att för varje stång, bestämma om den är dragen,
tryckt eller ospänd.
konvention
P
T traction C compression U unstressed
representerar en känd kraft representerar en
okänd kraft
krafterna som verkar på noden betraktas.
P
En metod är att ställa upp kvalitativa
jämviktsekvationen för knutpunkterna.
4
Byggnadsmekanik gk 11.4
P
N12 är kraften som stången 12 applicerar på nod
1. Med andra ord vill stången 12 dra noden 1
uppåt. Stången 12 är därför dragen.
Horisontell jämvikt den horisontella
komponenten av N13 måste motverka kraften P,
vilket ger tecknet för N13. N13 är kraften
som stången 13 applicerar på nod 1. Stången 13 är
därför tryckt.
T
C
När N13 är känd kan N12 bestämmas.
P
Vertikal jämvikt N12 måste motverka den
vertikala komponenten av N13, vilket ger tecknet
för N12.
5
Byggnadsmekanik gk 11.5
Exempel 2
3
2
P
När N13 är känd kan N12 bestämmas. Vertikal
jämvikt N12 måste motverka den kraften P,
vilket ger tecknet för N12. N12 är därför dragen.
P
P
3
2
T
U
Horisontell jämvikt den horisontella
komponenten av N13 är noll eftersom det är den
enda horisontella kraften som verkar på noden.
N13 är därför också noll.
P
6
Byggnadsmekanik gk 11.6
Exempel 3
Man kan fortsätta med nod 2
P
Horisontell jämvikt den horisontella
komponenten av N24 måste motverka N23. Det ger
N24 tryckt.
8 ekvationer 8 obekanta
Statiskt bestämt
Man måste börja med nod 3 eftersom det är den
enda nod med bara två obekanta krafter
N23 är dragen
P
N34 är ospänd
7
Byggnadsmekanik gk 11.7
Vertikal jämvikt N12 måste motverka den
vertikala komponenten av N24 . Det ger N12 dragen.
T
P
C
U
T
Man kan fortsätta med nod 1 och nod 4 för att
bestämma stödreaktionerna.
8
Byggnadsmekanik gk 11.8
Variant 1 tecknet för den vertikala reaktionen
vid nod 1 kan bestämmas direkt genom att betrakta
jämvikten av hela strukturen.
Variant 2 N24 kan bestämmas direkt genom att
göra ett snitt.
P
P
Den horisontella jämvikten av strukturens övre
del ger tecknet för N24.
Endast två krafter ger ett moment kring nod 4.
Den vertikala reaktionen vid 1 pekar därför
neråt.
P
9
Byggnadsmekanik gk 11.9
Exempel 4
N35 kan också bestämmas genom att betrakta den
vertikala jämvikten av nod 3.
P
10 ekvationer - 11 obekanta statiskt obestämt
av grad 1. Jämviktsekvationer räcker inte.
Det är omöjligt att fortsätta med
jämviktsekvationer. Man måste tänka på hur
strukturen deformeras. Ett sätt är att se att nod
5 går åt höger och därför är stängerna 15 och 25
dragna.
man kan ändå hitta några obekanta
Jämvikten av nod 4 ger N34 och N45 dragna.
P
10
Byggnadsmekanik gk 11.10
Hittills har vi hittat följande
Stödreaktionen vid nod 5 kan inte bestämmas genom
den kvalitativa jämvikten av denna nod. Man vet
inte om den vertikala komponenten av N25 är
större eller mindre än N35.
T
T
C
T
T
P
Nu kan man successivt fortsätta med nod 2 som ger
N12 och N23 tryckta, nod 1 som ger
stödreaktionerna vid 1, och nod 3 som ger
stödreaktionen vid 3.
Stödreaktionen vid 5 kan hittas genom att se att
noden går neråt om stöden tas bort. För att
motverka denna förskjutning behövs en kraft uppåt.
C
T
T
C
C
T
T
P
11
Byggnadsmekanik gk 11.11
Exempel 5
H4 V1 V4
P
P
För att kunna fortsätta måste man tänka på hur
strukturen deformeras. Ett sätt är att se att nod
3 går åt höger och därför är stängerna 23 och 13
dragna.
8 ekvationer 9 obekanta statiskt obestämt av
grad 1
De 3 reaktionerna kan bestämmas genom att
betrakta hela strukturen (statiskt yttre bestämt)
12
Byggnadsmekanik gk 11.12
T
P
T
T
P
T
C
Nu kan man fortsätta som vanligt med nod 2 (för
att bestämma N12 och N24), nod 3 (för att
bestämma N34) och nod 1 (för att bestämma N14).
T
C
C