Sn - PowerPoint PPT Presentation
1 / 15
Title: Sn
1
Elementary Particles
1) Introduction 2) Quantum numbers and their
conservation laws 3) Antiparticles 4) Strange
particles 5) Resonances 6) Hadron
structure 7) Quark model 8) Particles of
standard model
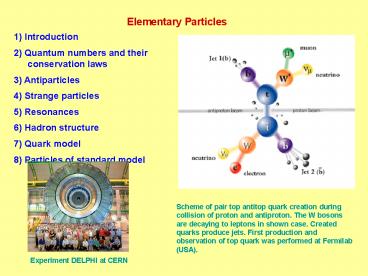
Scheme of pair top antitop quark creation during
collision of proton and antiproton. The W bosons
are decaying to leptons in shown case. Created
quarks produce jets. First production and
observation of top quark was performed at
Fermilab (USA).
Experiment DELPHI at CERN
2
Introduction
Four types of interactions gravitation,
electromagnetic, weak and strong.
Particle classification according to acting
interactions (gravitation acts on all particles )
Leptons interact weakly and charged also
electromagnetically, they do not interact
strongly (e, µ, t, ?e, ?µ, ?t) in the
present experiments they are point like
Hadrons interact in addition also strongly
they have structure and size 1 fm
Hadrons are divided to
Mesons - (p, p-, p0, K, K-, K0, ?, ?-,
?0) Baryons (p, n, ?, S, S-, S0, ?, ?, ?0,
?-, N, O-)
Particle classification according to statistics
Bosons Bose-Einstein statistic ? arbitrary
number of particles in given state integral
spin Wave function symmetric
?B(x1,x2,x3, ,xn) ?B(x2,x1,x3, ,xn)
Mesons and field particles (photons, gravitons,
gluons, )
Fermions Fermi-Dirac statistic ? Pauli
exclusion principle ? only one identical particle
in given state half-integral spin. Wave
function is antisymetric
?F(x1,x2,x3, ,xn) -?F(x2,x1,x3, ,xn)
Leptons and baryons
Antiparticles the same mass as particle,
opposite sign of quantum numbers (charge, baryon
number, lepton number, strangeness ). In the
most cases antiparticle is signed by overline
above appropriate symbol
but e- ?e, µ-?µ, t-?t
3
Conservation laws of quantum numbers
No existence of some reactions which are
energetically (kinematical) possible ? indication
of conservation law existence
No existing reactions with total charge
non-conservation ? charge conservation law
Number of fermions is conserved ? conservation
laws of baryon and lepton numbers
Baryon number if its conservation law is
strictly valid, proton (the lightest baryon) is
stable. We do not observe decay
p ? e p0
Single lepton numbers Le, Lµ a Lt
Necessity of introduction of lepton number
conservation law results from many experimental
evidences
No observed reactions
e- e- ? p - p -
Conservation law of single lepton numbers
µ- ? e- ? µ- ? e- e e-
Existed muon decay
Neutrino oscillations violation of single
lepton number conservation laws, total lepton
number is conserved.
Observation using solar neutrino detection by
Superkamiokande detector
Violation of total lepton number conservation
yet no observed
Violation of baryon number conservation law yet
no observed (sign of its existence is baryon
asymmetry of universe)
Such violation assume theories of interaction
unification.
4
Antiparticles
Particles with zero spin are relativistically
described by Klein-Gordon equation (linear
partial diferential equation of second order)
for particle motion direction in axe x
Its solution for free particle
We substitute
We obtain condition
Positive and negative solutions exist
Possible interpretation of solution E2 positive
energy, opposite charge ? antiparticle.
Leaving of interpretation, that intrinsic values
of Hamiltonian give energy of particle.
Similar situation is obtained for the Dirac
equation. Its solution describes particles with
spin 1/2.
In this case we have 4 solutions for wave
function
Particles with spin projection 1/2 a
1/2 Antiparticles with spin projection 1/2 a
1/2
Existence of electron and positron. Similarly
also for other fermions.
5
Discovery of first antiparticle
1932 - positron in cosmic rays 1955 antiproton
(BEVATRON), 1956 - antineutron
Simulation of electron positron pair creation
during gamma ray motion through electromagnetic.
Motion of created particles at magnetic field
Get together of particle and antiparticle ?
annihilation
Antiproton annihilation creation of K-, K0 a p
Annihilation and creation leptons
Annihilation and creation of quarks
6
Review of physical quantities from the view of
relation between particle and antiparticle
Quantity particle antiparticle
Mass m same same
Spin (magnitude) same same
Lifetime t same same
Isospin (magnitude) same same
Electric charge Q -Q
Magnetic moment µ -µ
Baryon number B -B
Lepton number L -L
Strangeness S -S
z component of isospin Iz Iz -Iz
Intrinsic parity P Same for bosons Opposite - fermions
Neutral particles
Fermions antiparticles are different in baryon
and lepton numbers Bosons if IBLS0 and µ0 ?
particle identical with antiparticle
7
Get together of particle and antiparticle ?
annihilation to photons and mesons
Conservation laws ? production of fermions in
pairs of particle-antiparticle.
For example reversal annihilation creation of
electron positron pairs during passage of photons
through electric field of nucleus
Antiparticles of most of known particles were
found.
Production of antiatoms (yet only antihydrogen),
production of antinuclei. ? existence of
antimatter
Production of antihydrogen in experiment ATHENA
Production of slow antiprotons at CERN
Charge conjugation symmetry - C-invariance
identity of processes during confusion between
particles and antiparticles and vice versa.
Violation of C-invariance and combined
CP-invariance
Existence of antimatter in the Universe in
cosmic rays only antiprotons and other
antiparticles produced by high energy proton
collisions.
Baryon asymmetry of universe excess of matter
above antimatter
8
Strange particles
1) New particles with much longer lifetime
10-10s they decay slowly, even if considerable
energy is released.
2) Production of these particles in pairs.
3) No existence of some types of decay
Existing decay S0 ? ?0 ?
S -1 -1 0
Non-existent decay S ? p ?
S -1 0 0
Sign of existence of new conservation law
strangeness conservation law (it is valid for
strong and electromagnetic interactions, it is
not valid for weak) ? introduction of quantity
strangeness (S)
Also for weak decay only ?S 1
Non-existent decay ?- ? n p -
S -2 0 0
Hyperon (strange baryon) ?- is decaying through
two steps
?-? ? p S -2 -1 0
? ? n p0 S -1 0 0
We introduce hypercharge Y B S
Isospin
Independency of strong interaction on charge. ?
proton and neutron are two charge state of single
particle nucleon. Value of isospin I is such,
that number of its projection to third axe 2I1
gives number of charge states.
Charge of hadrons
Q e(Iz Y/2) e(Iz (BS)/2)
9
First strange particles K mesons, lambda turn
of forties and fifties
Reaction of p - with nucleus in bubble chamber
produces K0 and ?
Production of O- (S2) particle picture of
bubble chamber at CERN
10
Resonances
Existence of very short living particles (typical
lifetime 10-23s) ? observed as resonance
structures in excitation functions
a) during particle scattering (for example p-N
scattering) b) during particle multiproduction
(resonance structures are studied in dependency
of cross section on invariant mass of scattering
system or produced particle system
Occurrence of resonance maxima with shape
described by Breit-Wigner function.
Width of maxima G is connected with lifetime t of
particle by Heisenberg uncertainty principle t
h/G. It defines also uncertainty in the particle
rest mass determination. Occurrence of resonances
for exactly given values of charge, isospin and
other quantum numbers ? particle.
Shape of resonance with M0 10 and G 3 above
constant background of cross section 1.0
11
Along quantum numbers ? baryon (nucleon, hyperon)
and meson (non-strange and strange) resonances
Nature of resonances very often excited states
of hadrons.
Short lifetime ? decay through strong interaction.
Hundreds of resonances are known totally.
Examples of resonances (only a few with
strangeness S 0)
Baryon resonances
N, N0 excited states of nucleons (structure
uud a udd) izospin I 1/2, strangeness S 0
? ? ?0 ? - - ? baryons and their excited
states (structure uuu, uud, udd a ddd), I 3/2,
S 0
Meson resonances
? meson and its excited state ?
excited states of ? mesons
Experimental problems background, resonance
overlapping, long decay lifetimes (smear of
resonance by measuring device response), very
short decay lifetime ? very broad resonances.
Simulation of meson resonances observation by
HADES spectrometer
12
Hadron structure
Evidences of hadron structure existence
1) Scattering experiments charge distribution
measured by high energy electrons (they do not
interact strongly) ? parton structure
2) Jets cluster of high energy particles
(hadrons) created during deep inelastic
scattering of quarks
3) Anomalous magnetic moments of nucleons
µp 2.792 µJ, µn -1.913 µJ
4) Excited states of hadrons (nucleons) of
proton (N), of neutron (N0) belong
to resonances different orbital moment of
constituents
5) Systematic of elementary particles
distribution to isospin multiplets (particle
masses at isospin multiplet are very similar)
Multiplet particles are placed in plane
characterized by isospin and hypercharge
Two examples of baryon multiplet
Explanation by three particle existence quarks
(actually by six three quarks and three
antiquarks) , from which elementary particles
consisted of.
13
Quark structure of hadrons
Baryons ? three quarks n udd, p uud, S
uus, S0 uds, ? uds, O sss (S0, ? differ by
isospin)
Mesons ? quark antiquark
Baryon decuplet (resonances)
Identical quarks (fermions) at ground state
Pauli exclusion principle ? necessity of new
quantum number color quantum chromodynamics
(QCD)
Additional particles ? three new quarks new
quantum numbers
Quark Q e I(JP) Iz S C B T
u 2/3 1/2(1/2) 1/2 0 0 0 0
d -1/3 1/2(1/2) -1/2 0 0 0 0
s -1/3 0(1/2) 0 -1 0 0 0
c 2/3 0(1/2) 0 0 1 0 0
b -1/3 0(1/2) 0 0 0 -1 0
t 2/3 0(1/2) 0 0 0 0 1
Review of quarks
14
Quark structure of proton
Colored quarks held together by strong
interaction (exchange of gluons transferring
color)
Discovery of O- particle by bubble chamber
at Brookhavenu laboratory
Very intensive field of strong interaction ?
complicated structure of vacuum virtual
quark-antiquark pairs and gluons
Picture of K meson creation and decay during
flight obtained by bubble chamber at CERN
15
Particles of standard model
Our understanding of matter structure and
interactions so far culminate in standard model.
Standard model includes all known fundamental
particles
1) Particles of matter quarks and leptons 2)
Particles of interactions intermediate bosons
(gluons, W, Z0, photon and Higgs boson)
Look as point like particles for accessible
energies.
Three families of leptons
Three families of quarks in different collors
where a red, green, blue
Quarks only bonded to colorless hadrons. Quarks
are directly observed
1) In high energy electron scattering on hadrons
(u,d) 2) As hadron jets during high energy deep
inelastic scattering transformation (decay)
and hadronisation of c, b and t quarks
The search of standard model particles was
completed during last years
1) Production and observation of quark t (in the
form of t, anti-t pairs) v r. 1995 Fermilab USA
(CDF and D0 experiments on Tevatron accelerator
with colliding beam of p, anti-p - vs 1.7 TeV),
last value of mt (1767) GeV/c2 2) Observation
of ?t neutrino at 2000 year at Fermilab USA
(E872 experiment - DONUT) 3) Sign of Higgs boson
existence at 2000 year by LEP at CERN
Schwitzerland (ALEPH, DELPHI, L3, OPAL), mass 115
GeV/c2 so far not unquestionable evidence
problem with background and statistical
significance of effect on background