Straight Line - PowerPoint PPT Presentation
Title:
Straight Line
Description:
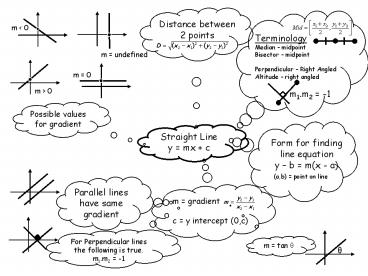
Possible values for gradient Straight Line y = mx + c Parallel lines have same gradient For Perpendicular lines the following is true. m1.m2 = -1 m = tan – PowerPoint PPT presentation
Number of Views:100
Avg rating:3.0/5.0
Title: Straight Line
1
Possible values for gradient
Straight Line y mx c
Parallel lines have same gradient
For Perpendicular lines the following is
true. m1.m2 -1
m tan ?
2
flip in y-axis
Move vertically up or downs depending on k
-
Stretch or compress vertically depending on k
y f(x) k
y f(-x)
Remember we can combine function !!
y kf(x)
Graphs Functions
y -f(x)
y f(kx)
y f(x k)
Stretch or compress horizontally depending on k
flip in x-axis
-
Move horizontally left or right depending on k
3
g(f(x))
But y f(x) is x2 - 4
f(x) x2 - 4
g(f(x))
x
y f(x)
Restriction
Domain
Range
x2 - 4 ? 0
A complex function made up of 2 or more simpler
functions
Similar to composite Area
(x 2)(x 2) ? 0
x ? 2
x ? -2
Composite Functions
But y g(x) is
f(g(x))
f(x) x2 - 4
f(g(x))
x
y g(x)
y2 - 4
Rearranging
Restriction
x2 ? 0
Domain
Range
4
Format for Differentiation / Integration
Surds
Indices
Basics before Integration
Working with fractions
5
Nature Table
Equation of tangent line
Leibniz Notation
Straight Line Theory
Gradient at a point
f(x)0 Stationary Pts Max. / Mini Pts Inflection
Pt
Graphs f(x)0
Derivative gradient rate of change
Differentiation of Polynomials
f(x) axn then fx) anxn-1
6
Completing the square f(x) a(x b)2 c
Easy to graph functions graphs
-2
-4
-2
Factor Theorem x a is a factor of f(x) if f(a)
0
2
1
0
1
(x2) is a factor since no remainder
f(x) 2x2 4x 3 f(x) 2(x 1)2 - 2 3 f(x)
2(x 1)2 1
If finding coefficients Sim. Equations
Discriminant of a quadratic is b2 -4ac
Polynomials Functions of the type f(x) 3x4
2x3 2x x 5
Degree of a polynomial highest power
Tangency
b2 -4ac gt 0 Real and distinct roots
b2 -4ac lt 0 No real roots
b2 -4ac 0 Equal roots
7
Limit L is equal to
Given three value in a sequence e.g. U10 , U11 ,
U12 we can work out recurrence relation
U11 aU10 b
U12 aU11 b
Use Sim. Equations
a sets limit b moves limit Un no effect
on limit
Recurrence Relations next number depends on the
previous number
Un1 aUn b
a gt 1
a lt 1
a gt 1 then growth a lt 1 then decay
Limit exists when a lt 1
b increase - b decrease
8
Remember to change sign to if area is below
axis.
Remember to work out separately the area above
and below the x-axis .
f(x)
g(x)
b
A ? f(x) - g(x) dx
Integration is the process of finding the AREA
under a curve and the x-axis
a
Area between 2 curves
Finding where curve and line intersect f(x)g(x)
gives the limits a and b
Integration of Polynomials
IF f(x) axn Then I f(x)
9
(No Transcript)
10
Addition Formulae sin(A B) sinAcosB
cosAsinB cos(A B) cosAcosB sinAsinB
Double Angle Formulae sin2A 2sinAcosA cos2A
2cos2A - 1 1 - 2sin2A
cos2A sin2A
Trig Formulae and Trig equations
3cos2x 5cosx 2 0
Let p cosx
3p2 5p - 2 0
(3p 1)(p -2) 0
sinx 2sin(x/2)cos(x/2)
cosx 2
p cosx 1/3
sinx 2 (¼ v(42 - 12) )
x no soln
x cos-1( 1/3)
x 109.5o and 250.5o
sinx ½ 2v15)
11
- Rearrange into sin
- Find solution in Basic Quads
- Remember Multiple solutions
Basic Strategy for Solving Trig Equations
Trigonometry sin, cos , tan
Amplitude
Complex Graph
Period
sin x
Basic Graphs
Amplitude
Amplitude
Period
Period
y 2sin(4x 45o) 1
Period
Max. Value 21 3
Period 360 4 90o
cos x
tan x
Amplitude 2
Mini. Value -21 -1
12
same for subtraction
Addition
2 vectors perpendicular if
Scalar product
Component form
Magnitude
Basic properties
scalar product
Vector Theory Magnitude Direction
Q
Notation
B
P
a
Component form
A
Vectors are equal if they have the same magnitude
direction
Unit vector form
13
Tail to tail
Angle between two vectors
properties
Vector Theory Magnitude Direction
Section formula
B
n
c
Points A, B and C are said to be Collinear if
B is a point in common.
m
b
a
14
Trig.
Harder functions Use Chain Rule
Rules of Indices
Polynomials
Differentiations
Factorisation
Graphs
Real life
Stationary Pts Mini / Max Pts Inflection Pts
Meaning
Rate of change of a function.
Straight line Theory
Gradient at a point.
Tangent equation
15
y logax
To undo log take exponential
y ax
To undo exponential take log
(a,1)
loga1 0
a0 1
(1,a)
(0,1)
logaa 1
(1,0)
a1 a
Basic log graph
Basic exponential graph
log A log B log AB
log (A)n n log A
Logs Exponentials
Basic log rules
y axb Can be transformed into a graph of the
form
y abx Can be transformed into a graph of the
form
log y x log b log a
log y b log x log a
Y mX C
Y mX C
Y bX C
Y (log b) X C
C log a
m log b
C log a
m b
16
f(x) a sinx b cosx
Compare coefficients
compare to required trigonometric identities
a k cos ß
Square and add then square root gives
b k sin ß
f(x) k sin(x ß) k sinx cos ß k
cosx sin ß
Process example
Divide and inverse tan gives
Wave Function
a and b values decide which quadrant
transforms f(x) a sinx b cosx into the
form
Write out required form
OR
Related topic Solving trig equations