Straight Line Equation. - PowerPoint PPT Presentation
Title:
Straight Line Equation.
Description:
... C = 2V + 3 From the graph we saw that : This was the number of squares you went up for each one you went along.This is called the gradient of the line. – PowerPoint PPT presentation
Number of Views:235
Avg rating:3.0/5.0
Title: Straight Line Equation.
1
Straight Line Equation.
y -2x 3
2
The Video Shop.
You join a video shop for a membership fee of 3
and then charges 2 for each video you hire
Complete the table below for the cost of hiring
different numbers of videos.
3
5
7
9
11
13
15
Now draw a graph of the table above.
3
Graph of videos hired against cost.
4
Now consider the structure of the graph.
The graph cuts the y axis at (0,3) because it
cost 3 to join the video shop before you hired
any videos.
For every square that you move to the right you
go two squares up because the cost of each video
is 2.
5
Finding A Formula.
Look at the table of values for the video hire
once again
Find a formula for the cost of videos (C) given
the number of videos (V)
C
2V 3
From the graph we saw that
6
Now repeat the question again for a video shop
charging 5 to join and 3 for each video
hired.Start by completing the table below.
Answer the questions below
Where does the graph cut the y axis ?
( 0 , 5 )
What is the gradient of the line
Gradient 3
The full graph is shown on the next slide
7
(No Transcript)
8
More About The Gradient.
The gradient (m) of a straight line is defined
to be
Change in vertical height.
Change in horizontal distance.
We are going to use this definition to calculate
the gradient of various straight lines
9
Find the gradients of the straight lines below
4
7
m
4
3
7
4
m
3
4
4
4
m
4
4
m 1
10
8
9
6
3
8
4
9
m
m
3
6
3
3
11
Negative Gradient
Consider the straight lines shown below
Can you split the lines into two groups based on
their gradients ?
Positive gradient
Lines (a) (c) and (d) slope upwards from left to
right.
Negative gradient
Lines (b) and (e) slope downwards from left to
right.
12
Calculate the gradients of the lines below
- 4
- 8
5
6
13
The Equation Of A Straight Line.
To find the equation of any straight line we
require to know two things
(a) The gradient of the line.
m gradient.
(b) The y axis intercept of the line.
c y axis intercept.
The equation of a straight line is
y m x c
Examples.
Give the gradient and the y axis intercept for
each of the following lines.
(1) y 6x 5
(2) y 4x 2
(3) y x - 3
m 6
c 5
m 4
c 2
m 1
c - 3
14
Finding The Equation.
Find the equation of the straight lines below
What is the gradient ?
m 1
What is the y axis intercept?
c 2
c 1
Now use y m x c
y x 2
15
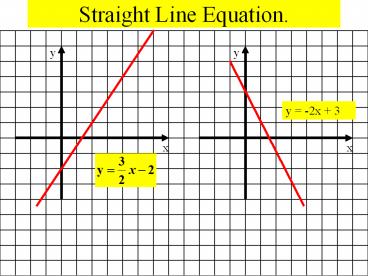
m -2
(3)
(4)
c 3
y -2x 3
c -2
16
c 2
c 6
17
The Gradient Formula.
The Gradient Formula.
It shows a straight line passing through the
points (x1,y1) and (x2,y2).
Look at the diagram below
We must calculate the gradient of the line using
the triangle shown
Change in vertical height
y2 y1
Change in horizontal distance
x2-x1
18
Calculate the gradient of the line through the
points below
(2) C(-4,8) and D(6,-10)
(1) A(4,6) and B( 10,12)
Solution
Solution
Write down the gradient formula
Substitute in your values
Calculate and simplify
19
Straight Line From Two Points.
Find the equation of the straight line passing
through (4,6) and (8,12)
Solution
Now substitute one of the points into y m x c
to find c.
Find the gradient of the line
Sub (4,6) into y 3x c
6 3 x 4 c
c 12 6
c - 6
Substitute gradient into y m x c.
Now write down the equation of the straight line
y 3 x c
y 3x - 6
20
Find the equation of a straight line passing
through C(6,-7) and D(-12,9)
Solution.
Now substitute one of the points into y m x c
to find c.
Calculate the gradient
Sub (6,-7) into equation
Substitute gradient into y m x c.
c -23
Equation of the straight line











![Solve Simultaneous Equations One Linear, one quadratic [Circle] PowerPoint PPT Presentation](https://s3.amazonaws.com/images.powershow.com/5861858.th0.jpg?_=20200807031)


















