Translation:slide Reflection:mirror Rotation:turn Dialation:enlarge or reduce - PowerPoint PPT Presentation
1 / 50
Title:
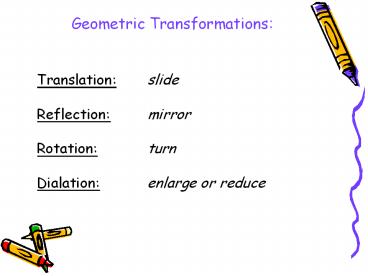
Translation:slide Reflection:mirror Rotation:turn Dialation:enlarge or reduce
Description:
Title: VECTORS Author: lpitman Last modified by: student Created Date: 11/1/2001 8:51:50 PM Document presentation format: On-screen Show Company: West Essex Regional ... – PowerPoint PPT presentation
Number of Views:191
Avg rating:3.0/5.0
Title: Translation:slide Reflection:mirror Rotation:turn Dialation:enlarge or reduce
1
Translation slideReflection mirrorRotation
turnDialation enlarge or reduce
Geometric Transformations
2
Pre-Image original figureImage after
transformation. Use prime notation
Notation
A
C
C
B
B
A
3
Isometry
- AKA congruence transformation
- a transformation in which an original figure and
its image are congruent.
4
Theorems about isometries
- FUNDAMENTAL THEOREM OF ISOMETRIES
- Any any two congruent figures in a plane can be
mapped onto one another by at most 3 reflections - ISOMETRY CLASSIFICATION THEOREM
- There are only 4 isometries. They are
5
TRANSLATIONmoves all points in a plane a
given direction a fixed distance
6
TRANSLATION VECTORDirectionMagnitude
PRE-IMAGE
IMAGE
7
Translate by the vector ltx, ygt
8
x moves horizontaly moves vertical
Translate by lt3, 4gt
9
Different notationT(x, y) -gt (x3, y4)
10
Translations PRESERVESizeShapeOrientat
ion
11
Reflectionover a line (mirror)
12
Properties of reflections
- PRESERVE
- Size (area, length, perimeter)
- Shape
- CHANGE
- orientation (flipped)
13
Reflect x-axis (a, b) -gt (a,-b)Change sign
y-coordinate
14
Reflect y-axis (a, b) -gt (-a, b)Change sign on
x coordinate
15
(No Transcript)
16
X-axis reflection
17
Y-axis reflection
18
PARTNER SWAPPart I (Live under my rules)
- Use sketchpad to graph label any three points
- Graph Reflect them over the line y x
- Graph-gtPlot new function-gtx-gtOK
- Construct two points on the line and connect them
- Mark this line segment as your mirror.
- WRITE a conjecture about how (a, b) will be
changed after reflecting over y x. Explain. - Repeat by reflecting over the line y -x. Write
a conjecture.
19
Starter
- Find one vector which would accomplish the same
thing as translating (3, -1) by lt3, 8gt then
applying the transformation T(x, y)-gt(x-4, y9) - Find coordinates of (7, 6) reflected over
- a.) the y-axis
- b.) the x-axis
- c.) the line y x
- d.) the line x -3
- 3. HW Check Peer edit
20
Rotations have
- Center of rotation
- Angle of rotation
21
Example Rotate Triangle ABC 60 degrees
clockwise about its center
- Find the image of A after a 120 degree rotation
- Find the image of A after a 180 degree rotation
- Find the image of A after a 240 degree rotation
- Find the image of A after a 300 degree rotation
- Find the image of A after a 360 degree rotation
22
Rotated 90 degrees counterclockwise
23
ROTATIONS PRESERVE
- SIZE
- Length of sides
- Measure of angles
- Area
- Perimeter
- SHAPE
- ORIENTATION
24
PARTNER SWAPPart II (Live under new rules)
- Use sketchpad to graph label any three points.
Connect them and construct triangle interior. - Rotate your pre-image about the origin 90?
- Rotate the pre-image about the origin 180?
- Rotate the pre-image about the origin 270?
- Rotate the pre-image about the origin 360?
- WRITE A CONJECTURE What are the coordinates of
(a, b) after a 90, 180, and 270 degree rotation
about the origin?
25
Rotations on a coordinate plane about the origin
- 90? (a, b) -gt (-b, a)
- 180? (a, b) -gt (-a, -b)
- 270? (a, b) -gt (b, -a)
- 360? (a, b) -gt (a, b)
26
DEBRIEFING
- Find the coordinates of (2, 5)
- Reflected over the x-axis
- Reflected over the y-axis
- Reflected over the line x 3
- Reflected over the line y -2
- Reflected over the line y x
- Rotated about the origin 180?
- Rotated about the origin 270 ?
- Rotated about the origin 360 ?
27
Review the rules for coordinate geometry
transformations
- Which two transformations would accomplish the
same thing as a 90 degree rotation about the
origin? - Use sketchpad to justify your answer
28
Coordinate Geometry rules
- Reflections
- x axis (a, b) -gt (a, -b)
- y axis (a, b) -gt (-a, b)
- yx (a, b) -gt (b, a)
- Rotations about the origin
- 90? (a, b) -gt (-b, a)
- 180? (a, b) -gt (-a, -b)
- 270? (a, b) -gt (b, -a)
- 360? (a, b) -gt (a, b)
29
GLIDE REFLECTIONS You can combine different
Geometric Transformations
30
Practice Reflect over y x then translate by
the vector lt2, -3gt
31
After Reflection
32
After Reflection and translation
33
Santuccis Starter
- Complete the following transformations on (6, 1)
and list coordinates of the image - a. Reflect over the x-axis
- b. Reflect over the y-axis
- c. Rotate 90 about the origin
- d. Rotate 180 about the origin
- e. Rotate 270 about the origin
- EXPLAIN in writing what two transformations
would accomplish the same thing as a 90 degree
rotation about the origin?
34
Starter
- Find the coordinates of pre-image (3, 4) after
the following transformations (do without
graphing) - reflect over y-axis
- reflect over x-axis
- reflect over yx
- reflect over y-x
- translate lt-2, 6gt
- rotate 90? about origin
- rotate 180? about origin
- rotate 270? about origin
- rotate 360? about origin
35
PAIRS Sketchpad Exploration
- Rotate (3, 4) 90 degrees about the point (1, 6).
What two transformations will produce the same
result? - Try it again by rotating (3, 4) 90 degrees about
(-2, 5). - Rotate (2, -6) 90 degrees about (1, 7)
- Describe OR LIST STEPS FOR how you can find the
image of any point after a 90? rotation about (a,
b). - Try it again with a 180? rotation about (a,b).
How can you find the image? - Try it again with a 270? rotation about (a,b).
How can you find the image?
36
Starter HW Peer edit Practice 12-5
- Reflectional symmetry
- Reflectional symmetry
- Both rotational and Reflectional symmetry
- Reflectional symmetry
- See key
- See key
- No lines of symmetry
- Line symmetry (5 lines) and 72 degree rotational
symmetry - Line symmetry (1 line)
- Line symmetry (4 lines) and 90 degree rotational
symmetry - Line symmetry (8 lines) and 45 degree rotational
symmetry - 180 degree rotational symmetry
- Line symmetry (1 line)
- Line symmetry (8 lines) and 45 degree rotational
symmetry - 180 degree rotational symmetry
- Line symmetry (1 line) 17-21 see key
37
Symmetry
- Line Symmetry
- If a figure can be reflected onto itself over a
line. - Rotational Symmetry
- If a figure can be rotated about some point onto
itself through a rotation between 0 and 360
degrees
38
What kinds of symmetry do each of the following
have?
39
What kinds of symmetry do each of the following
have?
Rotational (180) Point Symmetry
Rotational (90, 180, 270) Point Symmetry
Rotational (60, 120, 180, 240, 300) Point Symmetry
40
Isometry Wrap Up
- Sketchpad Activitiy 6 Symmetry in Regular
Polygons - Dilations Exploration
- NOTE TEST WILL BE END OF NEXT WEEK!!!
41
Dilations
- Plot any 5 points to make a convex polygon and
fill in its interior red. - Mark the origin as center.
- Make the polygon larger by a scale factor of 2
and fill it in green. - Make the polygon smaller by a scale factor of
1/3. Fill it in red. - Measure your coordinates and Explain how you can
find coordinates of a dilation image. - Try marking a new center and dilating a few
points. What is the center of a dilation? How
does it change the measurements?
42
Tessellations web-quest
- VISIT http//www.tessellations.org/tess-what.htm
- Explore read information underTessellations
- What are they
- The beginnings
- Symmetry MC Escher
- The galleries
- Solid Stuff
- Answer the following questions
- 1. What is symmetry and list the types
discussed. - 2. What are the Polya symmetries?
- 3. How many Polya symmetries are there?
- 4. What are the Rhomboid possibilities?
- 5. What is the difference between a periodic
and aperiodic tiling?
43
TO-DO
- Complete Tessellations Sketchpad explorations,
8, 9 - Read rubric and write questions. Begin design
44
INDIRECT PROOFIf q then p
- Assume that the conclusion is FALSE.
- Reason to a contradiction.
- If ngt6 then the regular polygon will not
tessellate. - ASSUME The polygon tessellates
- SHOW n can not be gt6
45
Indirect proof Regular polygons with ngt6 sides
will not tessellate
- Proof
- Assume a polygon with ngt6 sides will tessellate.
- This means that none interior ltmeasure will
equal 360 - IF n 3 there are 6 angles about center point
- IF n 4 there are 4 angles about center point
- IF n 6 there are 3 angles about center point
- Therefore, if ngt6 then there must be fewer than 3
angles about the center point. In other words,
there must be 2 or fewer. If there are 2 angles
about the center point then each angle must
measure 180 to sum to 360 - But no regular polygon exists whose interior
angle measures 180 (int. lt sum must be LESS than
180). Therefore, the polygon can not tessellate.
46
Santuccis Starter
- Determine if the following will tessellate
provide proof - Isosceles triangle
- Kite
- Regular pentagon
- Regular hexagon
- Regular heptagon
- Regular octagon
- Regular nonagon
- Regular decagon
47
Review practice
- Find the image of A(-1, 4) reflected over the
x-axis then over the y-axis (two intersecting
lines). What one transformation would accomplish
the same result? - Find the image of B(6, -2) reflected over x3
then over x-5 (two parallel lines). What one
transformation would accomplish the same result? - List all the rotational symmetries of a regular
decagon. - Draw a regular octagon with all its lines of
symmetry (on sketchpad).
48
Problem from HSPA test
49
Coordinate TransformationsMOAT game
- Groups of 3
- Write answer on white board and send one runner
to stand facing the class with representatives
from all other groups (hold board face down).
When MOAT is called flip answer so all members
seated can see answer. - 1st group correct 3 points
- 2nd group correct 2 points
- 3rd group correct 1 points
- Group with HIGHEST points 3 on quiz
- Group with 2nd highest points 2 on quiz
- Group with 3rd highest points 1 on quiz
50
HW Answers p. 650 10. H 11. M 12. C 13. Segment
BC 14. A 15. Segment LM 16. I 17. K 34. a.) B(-2,
5) b.) C(-5, -2) c.) D(2, -5) d.) Square 4
congruent sides angles
- 12-4
- 4. F translate twice the distance
- Translate T across m twice the distance between
l and m - V rotated 145
- 10-17. Peer edit
- opp reflection
- same translation
- same 270 rotation
- opp reflection
- Glide lt-2, -2gt, reflect over y x 1
- 28. Glide lt0, 4gt, reflect over y 0 (x-axis)